Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 2.3 - Ex. 48
48.Seja
- Encontre e .
- existe?
- Esboce o gráfico de .
Passo 1
Olá, meu querido colega. Vamos a resolução de mais uma atividade?
Aqui a gente tem uma função composta por duas equações, cada uma para um intervalo e a partir disso iremos calcular seus limites laterais, iremos decidir se o limite da função existe nesse ponto, como também iremos esboçar o gráfico da função.
Para calcularmos os limites laterais, devemos nos aproximar de , hora por valores infinitesimalmente maiores que , hora por valores infinitesimalmente menores que .
Casos esses limites laterais sejam iguais, teremos então que o limite existe, caso não seja, nosso limite não existe.
Passo 2
Para o item (a), temos o seguinte:
Como estamos vindo da esquerda, estamos no caso em que iremos nos aproximar de por valores . Logo, iremos escolher:
Assim,
Como não temos nenhuma indeterminação, podemos substituir:
Agora vamos analisar o seguinte caso:
Dessa vez estamos vindo da direita, isto é, iremos nos aproximar por valores . Logo,
Novamente, podemos substituir o valor para o cálculo do limite por não termos nenhuma indeterminação:
Passo 3
(b) Para existir , os limites laterais precisam ser iguais. Como os limites laterais são diferentes, não existe!
Passo 4
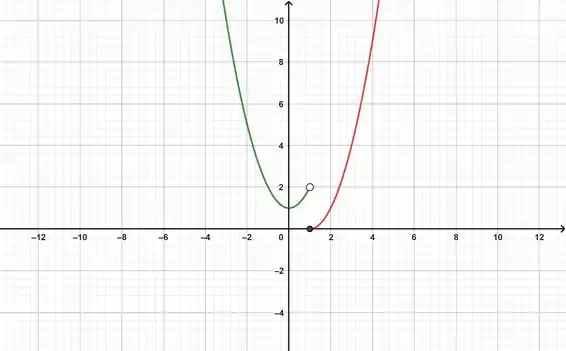
- Agora é só esboçarmos o gráfico
:
:
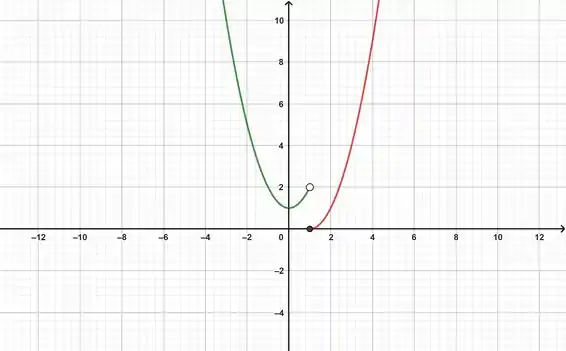
Veja que no gráfico o ponto , onde a gente tem a mudança de qual equação é definida. O ponto fechado indica que no ponto a função é definida por:
Já o ponto aberto diz que a função não é definida naquele ponto.
Resposta
- Não existe.
