Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 6.1 - Ex. 50
50. Uma cunha é cortada de um sólido com a forma de um cone circular reto e tendo um raio de base com 5cm e uma altura de 20cm, por dois planos contendo o eixo do cone. O ângulo entre os planos tem uma medida de 30°. Ache o volume da cunha.
Passo 1
Não entendeu nadinha? Senta aí que você vai ver que não é tão difícil assim.
Ilustrando o que a questão pediu:
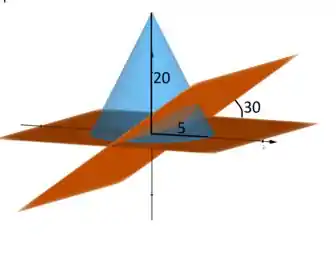
Para encontrar o volume pedido basta uma regra de três.
Um cone inteiro tem o volume de e um ângulo de 360° , já o pedaço de cone tem um ângulo de 30° e o volume é o que iremos descobrir.
Então,
Resposta
Exercícios de Livros Relacionados
Encontre o volume do sólido obtido pela rotação da região limitada pelas curvas dadas em torno das retas especificadas. Esboce a região, o sólido e um disco ou arruela típicos y = 1 / x ,x = 1 ,x = 2
Encontre o volume do sólido obtido pela rotação da região limitada pelas curvas dadas em torno das retas especificadas. Esboce a região, o sólido e um disco ou arruela típicos y = x ,y = 0 ,x = 2 ,x =
Encontre o volume do sólido obtido pela rotação da região limitada pelas curvas dadas em torno das retas especificadas. Esboce a região, o sólido e um disco ou arruela típicos y = ln x ,y = 1 ,y = 2
Encontre o volume do sólido obtido pela rotação da região limitada pelas curvas dadas em torno das retas especificadas. Esboce a região, o sólido e um disco ou arruela típicos y = 25 - x 2 ,y = 0 ,x =
Encontre o volume do sólido obtido pela rotação da região limitada pelas curvas dadas em torno das retas especificadas. y = x 3 ; y = x ; x ≥ 0 ; Em torno do eixo x .