Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 2.3 - Ex. 50
Seja
- Encontre e .
- existe?
- Esboce o gráfico de .
Passo 1
Falaiii galerinha do RA, bora resolver essa questão juntinho comigo?
Simboraaaa...
Na teoria dos limites em cálculo, um limite descreve o comportamento de uma função à medida que a variável independente (geralmente denotada por se aproxima de um certo valor. Especificamente, estamos interessados na situação em que se aproxima de um valor .Denotamos este limite como:
Isso significa que estamos olhando para o comportamento de quando se aproxima de .
Se o limite existe, ele descreve o valor que a função se aproxima à medida que se aproxima de
Existem dois conceitos importantes relacionados aos limites: limites laterais e o próprio limite.
Limites Laterais: Quando falamos sobre o limite de uma função em um ponto , geralmente estamos interessados em como a função se comporta à esquerda e à direita de . Estes são conhecidos como limites laterais.
Denotamos o limite da função à medida que se aproxima de pela esquerda como e o limite à medida que se aproxima de pela direita como o .
Passo 2
Existência de Limite: Dizemos que
existe se e somente se é igual a
Isso implica que a função tem um comportamento definido à medida que se aproxima de .
Passo 3
Para o item (a), temos o seguinte:
Como estamos vindo da esquerda, estamos no caso em que . Logo,
Assim,
Para :
Agora vamos analisar o seguinte caso:
Dessa vez estamos vindo da direita, isto é, . Logo,
Para :
Passo 4
Item (b) Para existir , os limites laterais precisam ser iguais.
Como os limites laterais são diferentes, não existe!
Passo 5
Item (c) Agora é só esboçarmos o gráfico!
Vamos agora desenhar o gráfico da função para visualizar melhor seu comportamento em torno do ponto
A função é definida como:
:
:
Para desenhar o gráfico, podemos dividir a função em duas partes distintas para os intervalos
Para
Nesse intervalo,
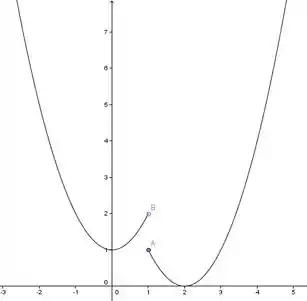
Esta é uma parábola com concavidade voltada para cima, passando pelo ponto como mostra a figura abaixo:
Para :
Nesse intervalo,
Esta é uma parábola com concavidade voltada para cima, com o vértice deslocado para a direita em 2 unidades, como mostra a figura abaixo:
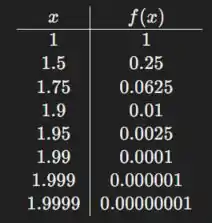
Agora, podemos unir essas duas partes para desenhar o gráfico completo de
A função possui uma descontinuidade em onde os limites laterais não são iguais.
Isso é evidenciado pela mudança repentina na função de para
O gráfico será uma parábola suave até , onde haveria um "salto" abrupto para outra parábola, como mostra o gráfico abaixo.
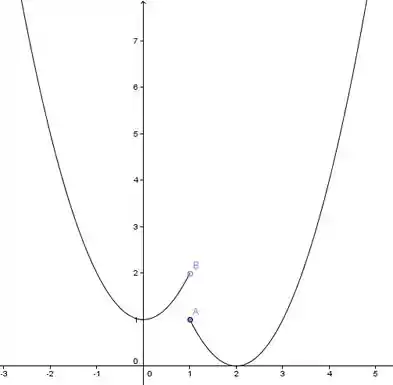
Resposta
- Não existe.
