Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 2.5 - Ex. 4
4. Do gráfico de , diga os intervalos em que é contínua.
Passo 1
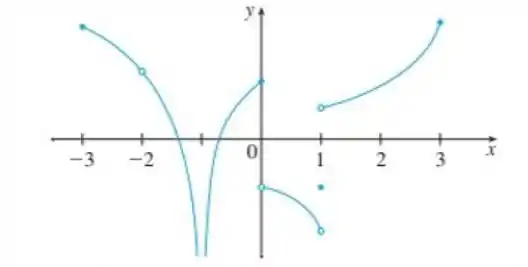
Opa, bora resolver essa questão?! O enunciado nos da o gráfico da função de :
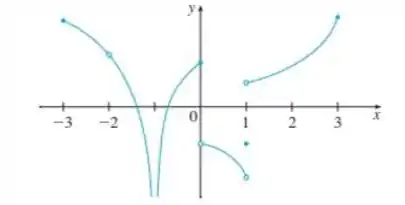
E pede pra a gente dizer onde a função é contínua!
Bem, uma função é contínua quando a gente consegue desenhar ela sem tirar o lápis do papel!
Tá, mas calma lá meu patrão, como a gente é malandro e sagaz, vamos primeiro encontrar o intervalo e as descontinuidades.
Passo 2
Vamos então analisar o gráfico:
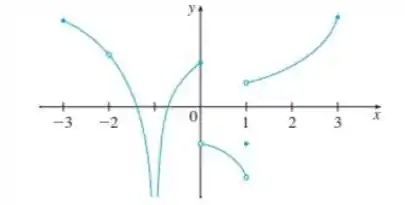
Nosso intervalo então vai de até , . Vamos ver da onde até onde a gente consegue desenhar sem tirar o lápis do papel:
- , temos uma bolinha aberta em ;
- , em ;
- ;
- , em e temos bolinha aberta;
- , em temos bolinha aberta.
Formalizando essas informações temos:
Prontinho!
Resposta
O intervalo é :
Exercícios de Livros Relacionados
A força gravitacional exercida pela Terra sobre uma unidade de massa a uma distância r do centro do planeta é F r = G M r R 3s erR G M r 2 s er ≥ R Onde M é a massa da Terra; R é seu raio; e G é a con
Para quais valores da constante c a função f é contínua em - ∞ , ∞ ? f x = { c x 2 + 2 xs ex2x 3 - c xs ex ≥ 2
Encontre os valores de a e b que tornam a função f contínua em toda a parte. f x = x 2 - 4 x - 2 s ex2 a x 2 - b x + 3s e2x3 2 x - a + b s ex ≥ 3 .
Demonstre que f é contínua em a se e somente se lim h → 0 f a + h = f ( a )
Para que valores de x a função f é contínua? f x = 0 s exér a c i o n a l 1 s exéi r r a c i o n a l é é