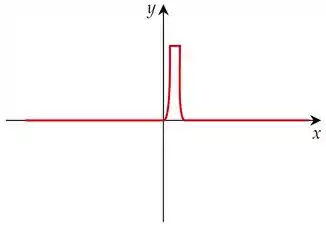
Trace ou copie o gráfico de . (Suponha os eixos com a mesma escala.) Use o método do Exemplo 1 para esboçar o gráfico de .
Passo 1
Faaala, gente bonita! Tudo certo?
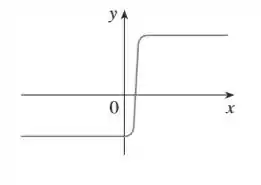
Essa questãozinha pede pra avaliarmos esse gráfico aqui:
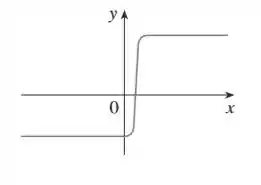
A partir daí, precisamos fazer um esboço do gráfico da sua derivada . Mas como fazemos isso?
O enunciado dá uma dica. Ele fala pra usarmos o mesmo método utilizado no Exemplo 1 do livro, que se baseia no fato de que podemos interpretar a derivada de uma função como a inclinação da reta tangente.
O método consiste em traçar retas tangentes em alguns pontos e usar estimativas pra inclinação dessas retas e traçar o gráfico da derivada baseado nessas estimativas.
Então, vamos nessa porque temos várias tangentes pra desenhar!
Passo 2
Vamos começar com o lado esquedo da curva:
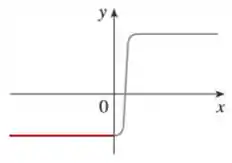
A derivada sempre estará em vermelho! Na figura acima, vemos que a reta tangente é totalmente horizontal. Isso significa que a derivada nesse intervalo, vai ser igual a .
Então, por enquanto, o gráfico da nossa derivada ficaria assim:
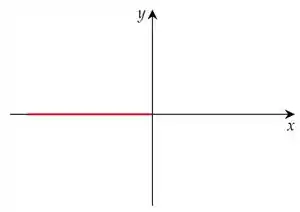
Vamos continuar a nossa análise!
Passo 3
Vamos checar a próxima parte do nosso gráfico:
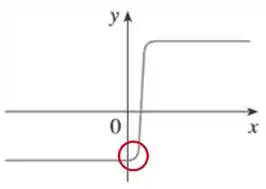
Vamos dar um zoom na região destacada e traçar algumas retas tangentes.

Podemos perceber que as inclinações da reta tangente vão ficando cada vez maiores, em um curto intervalo. Então podemos dizer que a derivada cresce rapidamente nesse intervalo.
Podemos representar no gráfico dessa forma:
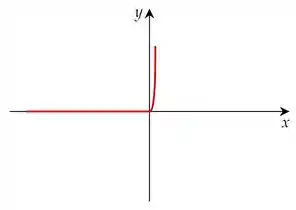
Muito bom! Vamos em frente!
Passo 4
Agora observa que a partir desse momento, o nosso gráfico fica com uma inclinação constante por um intervalo. Olha só:
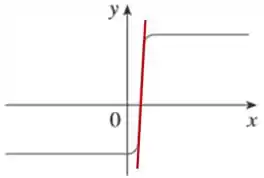
Se a inclinação é constante, isso significa que a derivada também vai ser constante nesse intervalo. Atualizando o gráfico, teríamos o seguinte:
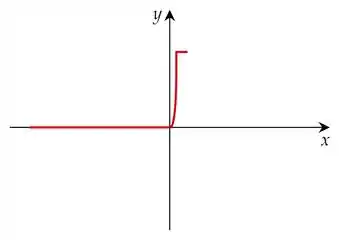
Observa que a inclinação é bem íngreme, mas não chega a ser vertical. Então comprovamos que a derivada deve ser uma constante positiva e com um valor relativamente alto.
Estamos quase lá!
Passo 5
A próxima região que vamos olhar é essa aqui:
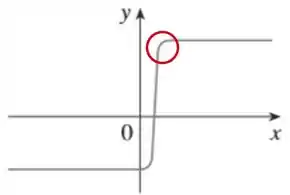
Análogo ao estudo que fizemos no passo 3, podemos observar que a inclinação das retas tangentes diminui rapidamente nessa região até se aproximarem de uma reta horizontal.
Então podemos dizer que a derivada diminui rapidamente até atingir o valor . Olha só:
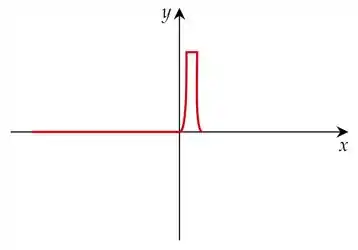
Falta só mais uma região pra avaliarmos! Pra cima deles!
Passo 6
Pra fechar, vamos checar a última região:
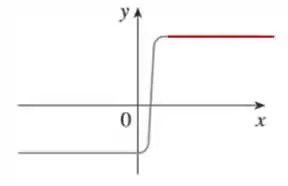
Novamente, temos uma reta tangente totalmente horizontal. Isso significa que a derivada nesse intervalo vai assumir o valor . O nosso gráfico da derivada vai ficar assim:
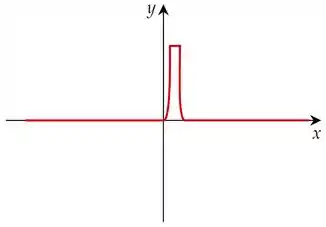
Uhuuuul! Conseguimos fechar o esboço da nossa derivada!
Partiu próximo!
Resposta
Esboço de :