Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 7.2 - Ex. 58

58. Encontre a área da região delimitada pelas curvas dadas

y = tan ⁡ x ,     y = tan ² ⁡ x ,     0 ≤ x ≤ π / 4

Passo 1

Pra facilitar a visualização, podemos esboçar um gráfico das duas funções

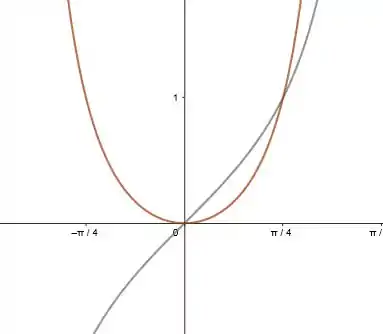
Onde a função f x = tan ⁡ x está em azul e a função g x = tan 2 ⁡ x está em vermelho. Logo a área será dada pela integral:

A = ∫ 0 π / 4 f x - g ( x ) d x = ∫ 0 π / 4 tan ⁡ x - tan 2 ⁡ x d x

Passo 2

Show de bolinhas, vamos dividir essa integral e resolver elas separadamente, desse jeito ó:

∫ 0 π / 4 tan ⁡ x - tan 2 ⁡ x d x = ∫ 0 π / 4 tan ⁡ x d x - ∫ 0 π / 4 tan 2 ⁡ x d x

A integral de tan ⁡ x já é conhecida pela gente né:

∫ ⁡ tan ⁡ x   d x = ln ⁡ sec ⁡ x

Já para tan ² ⁡ x , podemos fazer o seguinte:

∫ tan ² ⁡ x d x = ∫ sin 2 ⁡ x cos ² ⁡ x d x = ∫ 1 - cos ² ⁡ x cos ² ⁡ x d x = ∫ 1 cos ² ⁡ x - 1 d x

∫ sec ² ⁡ x - 1 d x

E aqui que vem a malandragem, porque sec ² ⁡ x , possui uma primitiva, já que :

d tan ⁡ x d x = sec 2 ⁡ x

tan ⁡ x = ∫ sec ² ⁡ x   d x

Portanto, temos:

∫ sec ² ⁡ x - 1 d x = tan ⁡ x - x

Passo 3

Iradoso né não, isso quer dizer então que nossa área é dada por:

A = ∫ 0 π / 4 tan ⁡ x - tan 2 ⁡ x d x = ln ⁡ sec ⁡ x - tan ⁡ x + x 0 π 4

A = ln ⁡ sec ⁡ π 4 - tan ⁡ π 4 + π 4 - ln ⁡ sec ⁡ 0 - tan ⁡ 0 + 0

A = ln ⁡ 2 - 1 + π 4 - 0 - 0 + 0

A = ln ⁡ 2 - 1 + π 4

Resposta

A = ln ⁡ 2 - 1 + π 4

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

É dada informação sobre o movimento de uma partícula ao longo de um eixo. (a) Use um CAS para encontrar a função posição da partícula com t≥0 . (b) Faça o gráfico da curva posição versus tempo. a t =
É dada informação sobre o movimento de uma partícula ao longo de um eixo. (a) Use um CAS para encontrar a função posição da partícula com t≥0 . (b) Faça o gráfico da curva posição versus tempo. v t =
Calcule a integral. ∫ 0 1 2 a r c s e nxd x
Calcule a integral. ∫ t g 5 4 x sec 4 ⁡ ( 4 x )
Calcule a integral. ∫ s e n 2 2 x cos 3 ⁡ 2 xd x