Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 7.6 - Ex. 85

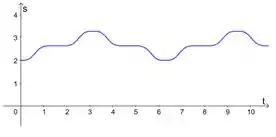
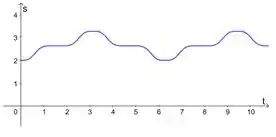
É dada informação sobre o movimento de uma partícula ao longo de um eixo.

(a) Use um CAS para encontrar a função posição da partícula com t   ≥   0 .

(b) Faça o gráfico da curva posição versus tempo.

v t = 20 cos 6 ⁡ t   s e n 3   t ,     s 0 = 2

Passo 1

(a) Para resolver essa a gente precisa lembrar que:

v t = s ' t ∴ s t = ∫ v ( t ) d t

Substituindo a expressão da velocidade, vamos usar a calculadora CAS do Geogebra para resolver a integral:

s t = ∫ 20 cos 6 ⁡ t   s e n 3   t d t

Fica assim:

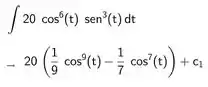
Para descobrir esse c 1 é só usar a informação dada no enunciado:

s 0 = 2

s t = 20 1 9 cos 9 ⁡ t - 1 7 cos 7 ⁡ t + c 1

s 0 = 20 1 9 cos 9 ⁡ 0 - 1 7 cos 7 ⁡ 0 + c 1 = 2

20 9 - 20 7 + c 1 = 2 ∴ c = 166 33

Logo, a função posição fica:

s t = 20 1 9 cos 9 ⁡ t - 1 7 cos 7 ⁡ t + 166 63

Passo 2

(b) Só a gente plotar o gráfico dessa função agora. Fica assim:

Resposta

  1. s t = 20 1 9 cos 9 ⁡ t - 1 7 cos 7 ⁡ t + 166 63
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule a integral13. ∫ sin ⁡ 2 x cos ⁡ 3 x d x
Calcule a integral: ∫ c o t g 2 3 t sec ⁡ 3 t d t
Calcule a integral: ∫ sec 5 ⁡ x d x
Calcule a integral: ∫ 0 π 8 t g 2 2 x d x
Calcule a integral: ∫ t gx sec 3 2 ⁡ x d x