Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Diomara - Cálculo Diferencial e Integral de Funções de Várias Variáveis- Ed: 3º - Capítulo 3.2 - Ex. 5b

5-Considere a superfície z = f ( x ,   y ) , onde:

f x ,   y = 8 - x 2 - y 2 ,     x 2 + y 2 ≤ 4 4 ,     x 2 + y 2 ≥ 4

Pede-se:

b)Um esboço da superfície.

Passo 1

b)Galera, quando x 2 + y 2 ≤ 4 nós temos um parabolóide elíptico definido pela seguinte expressão:

z = 8 - x 2 - y 2

Bom, podemos concluir que ele tem a concavidade voltada para baixo e vértice ( 0,0 , 8 ) , né ?!

Para x 2 + y 2 ≥ 4 , nós temos um plano z = 4 .

Assim, temos a seguinte superfície:

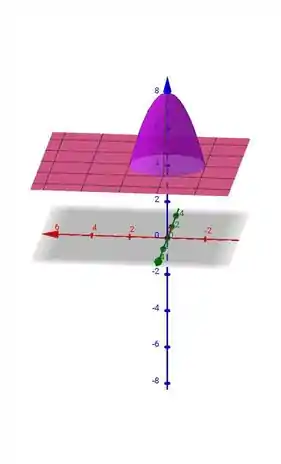
Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Identificar as afirmações verdadeiras:i) Todos os pontos de um conjunto aberto A são pontos de acumulação de A .
Identificar as afirmações verdadeiras:a) A união de bolas abertas é um conjunto conexo.
Repetir o exercício 2 para o conjunto: B = x ,y ,z ∈ R 3 - 1x1 ;- 1y1 ;- 1z1 }
7-Nas figuras 3.7 (i) e (ii), estão representadas, respectivamente, curvas de nível e superfícies de nível das funções f ( x ,y ) e g x ,y ,z . Escreva expressões adeuqdas para f e g .