Enunciado
Cálculo - Diomara - Cálculo Diferencial e Integral de Funções de Várias Variáveis- Ed: 3º - Capítulo 3.2 - Ex. 7
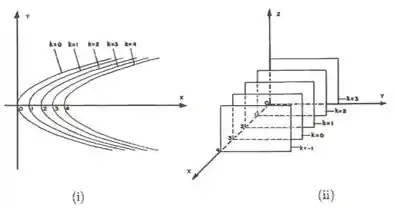
7-Nas figuras 3.7 (i) e (ii), estão representadas, respectivamente, curvas de nível e superfícies de nível das funções e Escreva expressões adeuqdas para e
Passo 1
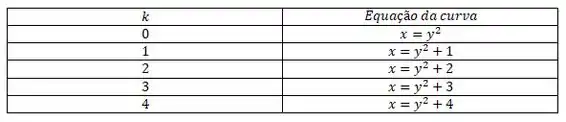
Na figura (i), nós observamos que para temos parábolas no seguinte formato que podem ser escritas dessa forma:
Assim, temos:
Isso é fácil de perceber montando essa tabela:
Passo 2
Na figura (ii), o nível parece ser o plano . Isso pode ser facilmente percebido por meio da tabela abaixo:
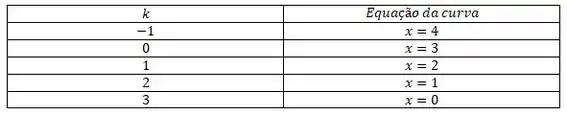
Dessa forma,
Resposta
Exercícios de Livros Relacionados
Representar graficamente os seguintes subconjuntos de R 2 . Identificar os conjuntos abertos. { x , y ∈ R 2 | x 2 - 4 x + y 2 ≥ 0 }
Seja A = { x ,y ∈ R 2 | 0x 2 + y 2 + 2 y + 11 } . Verificar se os pontos: a )0 ,- 1 2 b )( 0 ,- 1 ) c )( - 1 ,- 1 ) d )( 1 ,1 ) e )( 0 ,0 ) f ( 3 ,4 ) são pontos de acumulação de A .
Identificar as afirmações verdadeiras:h) O conjunto x ,y ∈ R 2 x ,y ∈ Q } não tem ponto de acumulação.
Verificar se o conjunto A = x ,y ∈ R 2 x , y ∈ N tem ponto de acumulação.
Identificar as afirmações verdadeiras:j) Se A é um conjunto aberto, nenhum ponto da fronteira de A pertence a A .