Enunciado
Cálculo - Diva Flemming - Cálculo B - Ed: 2º - Capítulo 3.7 - Ex. 3
Repetir o exercício para o conjunto:
Passo 1
Vamos tentar imaginar que parada é essa aí: primeiro pega duas das letras, só no plano , por exemplo. A desigualdade para fica:
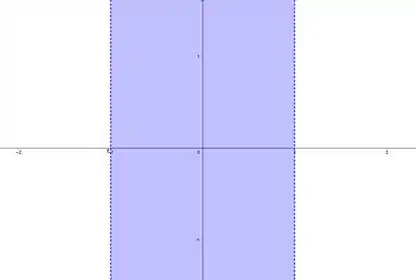
E a desigualdade em y:
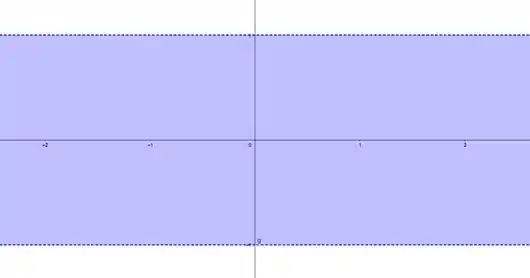
Intersectando os dois:
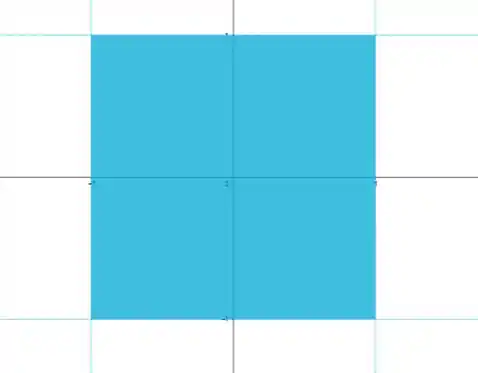
Então basicamente ficamos com um quadradinho, aberto nos cantos, de lado igual a e centro na origem.
Passo 2
Falta colocar a desigualdade de . Bom, o que vai acontecer é que a gente vai ficar empilhando várias dessa figura que encontramos no plano , para todo o espaço entre . O que dá quando a gente vai empihando vários quadradinhos, e ainda por cima, por um espaço do mesmo tamanho que antes, ou seja, de comprimento ? Vamos chegar em um cubo! Como as três desigualdades estão abertas, esse nosso cubo não vai ter a bordinha, então vai ser um conjunto aberto!
Passo 3
Só pra dar uma pensada nos vértices do cubo: o nosso quadrado tinha vértices em , , e . Assim, o nosso cubo vai ter seus oito vértices análogos a esses, mas adicionando as componentes em . Ficamos com os vértices , , , , , , e .
Resposta
Cubo aberto, de vértices , , , , , , e .