Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 8.5 - Ex. 62

62 - A supervisora do departamento de contabilidade de sua empresa pediu a você que encontrasse uma fórmula para o cálculo do estoque de gasolina nos tanques da empresa no fim do ano que pudesse ser utilizada por ela em um programa de computador. Um tanque típico tem a forma de um cilindro circular de raio r e comprimento L montado horizontalmente, como mostramos a seguir. Os dados chegam ao escritório de contabilidade como medidas de profundidade tiradas com uma vara de medição na vertical, marcada em centímetros.

A - Mostre, na notação da figura, que o volume de gasolina que enche o tanque a uma profundidade d é:

V = 2 L ∫ - r - r + d r 2 - y 2   d y

B – Calcule a Integral:

Passo 1

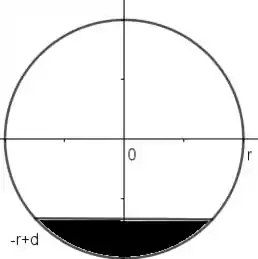
Observamos o círculo gerado, plotando a função para um raio qualquer, temos que o volume da parte preenchida é igual a multiplicação do comprimento do tanque com a área da região colorida acima.

Se considerarmos uma camada de gasolina com uma espessura qualquer localizada em:

- r < y < - r + d . Sendo a altura desta camada: 2 r 2 - y 2 , deste modo a área será:

A = 2 ∫ - r - r + d r 2 - y 2   d y

Temos assim que volume será: C o m p r i m e n t o   L × Á r e a   A

Assim:

V = L × 2 ∫ - r - r + d r 2 - y 2   d y

Deste modo o volume será:

V = 2 L ∫ - r - r + d r 2 - y 2   d y

Passo 2

Agora resolveremos o item b:

V = 2 L ∫ - r - r + d r 2 - y 2   d y

Resolveremos primeiro a integral como indefinida:

∫ r 2 - y 2   d y

Utilizaremos a fórmula 45 da página 630, que diz o seguinte:

∫ a 2 - x 2   d x = x 2 a 2 - x 2 + a 2 2 s e n - 1 x a + C

Subsittuindo na nossa integral:

∫ r 2 - y 2   d y = y 2 r 2 - y 2 + r 2 2 s e n - 1 y r + C

Inserindo os limites de integração:

2 L y 2 r 2 - y 2 + r 2 2 s e n - 1 y r + C - r - r + d

Assim:

2 L - r + d 2 r 2 - - r + d 2 + r 2 2 s e n - 1 - r + d r - - r 2 r 2 - - r 2 + r 2 2 s e n - 1 - r r  

Temos que:

s e n - 1 - r r = s e n - 1 - 1 =   - π 2

2 L - r + d 2 r 2 - d 2 + 2 d r - r 2 + r 2 2 s e n - 1 d - r r - - r 2 r 2 - r 2 + r 2 2 ⋅ - π 2

2 L - r + d 2 - d 2 + 2 d r + r 2 2 s e n - 1 d - r r - 0 - r 2 π 4

Desta forma:

2 L d - r 2 2 d r - d 2 + r 2 2 s e n - d - r r + r 2 π 4

Poderemos inserir alguns termos em evidência:

2 L d - r 2 2 d r - d 2 + r 2 2 s e n - 1 d - r r + π 2

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Use o resultado do Exercício 19 para determinar os centroides dos triângulos cujos vértices aparecem nos Exercícios 20-24. Considere a ,b0 . 24 - 0,0 ,0 , a ,( a 2 , b )
Use o resultado do Exercício 19 para determinar os centroides dos triângulos cujos vértices aparecem nos Exercícios 20-24. Considere a ,b0 . 21 - 0,0 ,1,0 ,( 0,1 )
25 - Densidade constante Determine o momento em torno do eixo x de um fio de densidade constante que se situe ao longo da curva y = x de x = 0 até x=2 .
26 - Densidade constante Determine o momento em torno do eixo x de um fio de densidade constante que se situe ao longo da curva y = x 3 de x =0 a x = 1 .
27 - Densidade variável - Suponha que a densidade do fio do Exemplo 4 seja δ = ks e n θ (k constante). Determine o centro de massa.