Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 7.Revisão - Ex. 64
64. Ache o volume do sólido de revolução gerado pela rotação da região limitada pela curva e pelas retas e em torno do eixo x.
Passo 1
Primeiro vamos visualizar a figura que está sendo rotacionada, a imagem a seguir mostra a figura.
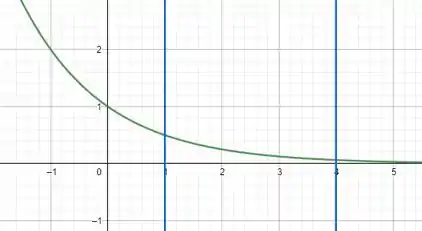
Vamos resolver esse problema usando o método dos discos.
Como essa figura está girando em torno da reta x, nosso disco imaginário estaria na vertical e a espessura do disco é dx, então temos que:
Então como o depende de precisamos achar R em termos de x.
Assim:
Logo:
Os limites de integração são esses já que x varia de 1 a 4 na região limitada.
Passo 2
Agora vamos resolver a integral.
Podemos escrever o integrando da seguinte maneira:
Assim:
Passo 3
Para continuar a resolver a integral vamos fazer a seguinte substituição:
Nossa integral toma a seguinte forma:
Para continuar a resolução vamos voltar a variável original.
Resposta
O volume do sólido de revolução é: