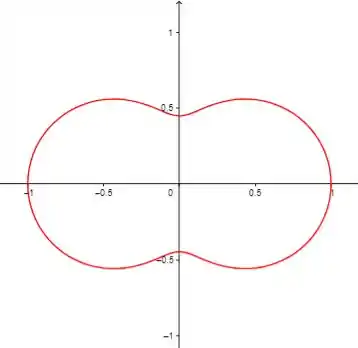
Use uma ferramenta gráfica para traçar a curva polar. Escolha o intervalo do parâmetro para ter certeza de que você fez a curva inteira.
(hipopédia)
Passo 1
Oie, vou te ajudar a resolver essa atividade hoje. Vem comigo!!
Aqui a gente precisa utilizar de uma ferramente gráfica para traçar o gráfico da curva polar:
Aqui a gente vai utilizar o GeoGebra, ele é online e gratuito e isso ajuda bastante.
Neste site, a única diferença é que usaremos o parâmetro no lugar de , mas isso não muda o resultado, basta considerar .
Para saber se o intervalo está traçando toda a curva, basta testar com um intervalo de a múltiplos de .
Passo 2
Para esse gráfico o intervalo usado foi
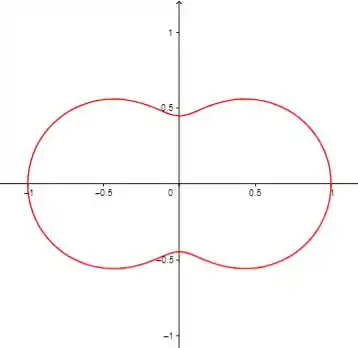
A periodicidade de é .
Portanto, você pode escolher o intervalo para .
Na verdade, você pode escolher qualquer intervalo de comprimento maior que para obter o gráfico completo.
Porque é uma função periódica de .
Resposta