Enunciado
Cálculo - Diomara - Cálculo Diferencial e Integral de Funções de Várias Variáveis- Ed: 3º - Capítulo 4.2 - Ex. 6
6-Num círculo de raio R, traçam-se duas cordas paralelas, em cima e outra abaixo do centro, e constrói-se um trapézio isósceles. Determinar as distâncias das duas cordas ao centro, para que a área do trapézio seja máxima.
Passo 1
Sou só eu que acho que ter uma figura que represente a situação do problema iria ajudar muito ?! Não, né ?!
Então, aqui está a nossa circunferência com o trapézio isósceles.
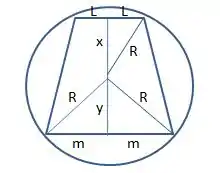
Como representado na imagem, se nós dividirmos a nosso trapézio ao meio, nós, consequentemente, dividimos as bases dele ao meio (isso porque ao formamos um triângulo isósceles com qualquer uma das bases e os raios, a mediana e a altura coincidem). Esquecendo um pouco essa parte geométrica (que é meio chatinha), temos agora que encontrar a área do nosso trapézio, né ?!
Passo 2
Dos triângulos retângulos que nós temos podemos tirar isso aqui:
E
Com isso, a área do nosso trapézio fica assim:
Ficou feio, né ?! Calma que depois só piora.
Passo 3
Agora, vamos para parte mais cremosa da questão. Não tem como falar de área máxima sem calcular os pontos críticos, né ?! Então, vamos encontrá-los!
A pergunta que fica é: Como resolver esse negócio ??? Eu sugiro que façamos o seguinte:
Substituindo isso na segunda equação, temos:
Portanto,
Passo 4
Se pegarmos essa relação que encontramos e substituirmos em , temos:
Lembrando que , já que é a altura do nosso trapézio.
Por fim,
Parece que é o fim, mas não é tah ?! Ainda temos que encontrar o
Substituindo
Agora sim, acabamos!
Até a próxima, galera.