Enunciado
Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 3.5 - Ex. 72
72. A tabela fornece a população dos Estados Unidos de e .
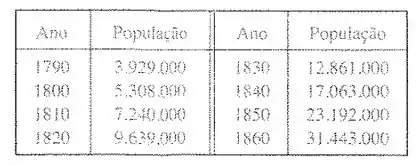
- Use uma calculadora gráfica ou computador para ajustar uma função exponencial aos dados. Faça um gráfico dos pontos dados e do modelo exponencial. Qual a qualidade do ajuste?
- Estime as taxas de crescimento em e fazendo a média de inclinações de retas secantes.
- Use o modelo exponencial da parte (a) para estimar as taxas de crescimento em e . Compare essas estimativas com as da parte (b)
Passo 1
(a)
Usarei o Excel como calculadora gráfica! E pelo excel a função que melhor se ajusta a essa tabela é:
Passo 2
(b) Com o gráfico traçado fica mais fácil né?
Faremos a mesma coisa para o ano de !
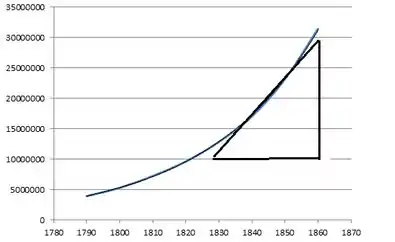
Como é uma estimativa diremos que vai até o !!
Passo 3
Agora acabou a estimativa vamos para a realidade, e ela é cruel!!!
Vamos derivar a expressão da População.
Vamos usar a regra da cadeia!
Isolando e já derivando!
Isolando e já derivando
Substituiremos por e com o auxilio da calculadora acharemos:
Substituiremos por e com o auxilio da calculadora acharemos:
O estimado ficou bem distante do “real” isso aconteceu, pois usamos eixos com poucas partições e retas secantes bem inclinadas!
Resposta
(a)
(b)
(c)
Exercícios de Livros Relacionados
Encontre a derivada da função.y = e^(k tg sqrt(x))
Encontre a derivada da função.f ( t ) = sqrt((t)/(t^2 + 4))
Encontre a derivada da função. y = cos 1 - e 2 x 1 + e 2 x
Encontre a derivada da função. y = 2 3 x ² ²
Encontre a derivada da função. y = cos sen tg π x