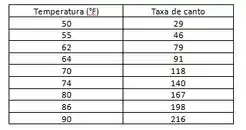
Biólogos observaram que a taxa de canto dos grilos de uma certa espécie aparentemente está relacionada com a temperatura. A tabela mostra as taxas de canto para várias temperaturas.
(a) Faça um diagrama de dispersão dos dados.
(b) Encontre e faça um gráfico da reta de regressão.
(c) Use o modelo linear da parte (b) para estimar a taxa de cantos a .
Passo 1
Fala, galera! Beleza? Vamos resolver essa questão!
O enunciado nos dá uma tabela e pede pra gente fazer um diagrama de dispersão de dados, a partir dela, fazer um gráfico da reta de regressão linear e usar esse modelo linear para estimar a taxa de cantos a .
A tabela que ele nos deu é essa daqui:

Ela relaciona a temperatura com a taxa de canto de uma espécie de grilos. A primeira coisa que devemos fazer é um gráfico de dispersão, que é uma representação desse conjunto de dados! Pra isso, nós vamos usar a temperatura como eixo horizontal e a taxa de canto como eixo vertical e marcar um ponto para cada linha da tabela, de acordo com a numeração dada.
Depois, nós vamos pegar o primeiro e o último pontos dados na tabela e calcular a inclinação da reta da forma:
Onde é a taxa de canto final, a taxa de canto inicial, a temperatura final e a temperatura inicial.
Com essa inclinação, vamos construir a reta de regressão linear usando a equação geral da reta:
Onde é a inclinação calculada e é um ponto conhecido do nosso gráfico.
Então, vamos comparar o resultado obtido com a regressão linear dada por uma ferramenta gráfica e depois vamos apenas substituir na equação da reta para obter o valor da taxa de canto nessa temperatura e responder o último item da nossa questão.
Vamos lá!
Passo 2
Vamos começar desenhando o nosso gráfico com a temperatura no eixo horizontal e a taxa de canto no eixo vertical e vamos marcar os pontos , , , , , , e .
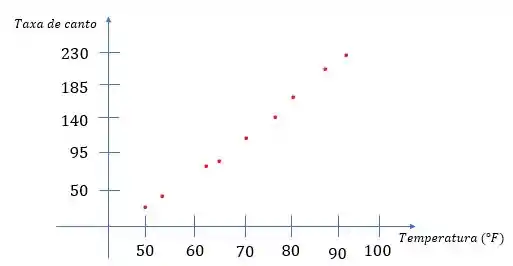
Esse é o nosso diagrama dispersão. Repare que os pontinhos são formados pelos dados da tabela e que se aproximam muito da forma de uma reta.
Passo 3
Agora vamos encontrar a reta de regressão linear a partir do gráfico anterior, para responder a letra (b).
Nós vimos no passo que a equação da reta pode ser dada na forma:
Onde representa a taxa de canto, a temperatura, a inclinação da reta e é um ponto conhecido do nosso gráfico.
Pra calcular essa inclinação , vamos usar o primeiro e o último ponto do gráfico anterior, e , respectivamente. Assim, vamos ter:
Calculando, obtemos:
Agora usando o ponto e a inclinação calculada e substituindo na equação da reta, vamos ter:
Aplicando a distributiva no produto do lado direito da equação:
E isolando :
Passo 4
Então, traçamos a reta de regressão no gráfico:
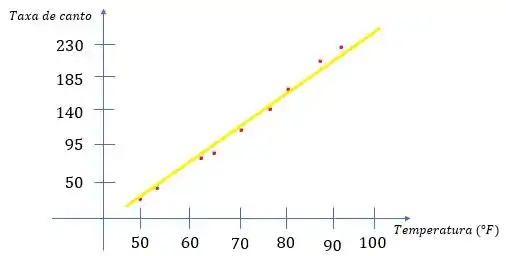
Se a gente usasse uma ferramenta computacional para traçar esse gráfico e obter a reta de regressão linear a partir dos pontos dados, nós teríamos algo assim:
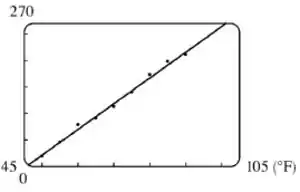
E a equação da reta de regressão dada por:
Que é bem próximo do cálculo que nós fizemos, mostrando que essa é uma boa aproximação.
Passo 5
Para a letra (c) é só substituirmos o valor de na equação da regressão obtida no passo . Assim, sendo , teremos:
Calculando o produto:
Logo,
Se a gente usasse a equação obtida pela ferramenta gráfica, teríamos:
Valeu, galera! Até a próxima! 😉
Resposta
(a)
(b)
(c)