Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 5.3 - Ex. 83a

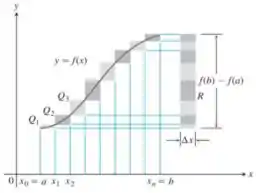
83. a) Suponhamos que o gráfico de uma função contínua f ( x ) suba gradualmente conforme x se move da esquerda para a direita em um intervalo [ a ,   b ] . Seja P uma partição de [ a ,   b ] em n subintervalos de comprimento ∆ x = b - a n . Observando a figura a seguir, demonstre que a diferença entre as somas superior e inferior para f nessa partição pode ser representada graficamente como a área de um retângulo R , cujas dimensões sejam f b - f a por ∆ x . (Dica: a diferença U - L é a soma das áreas dos retângulos diagonais Q 0 ,   Q 1 ,   Q 1 Q 2 ,   …   , Q n - 1 Q n situam-se ao longo da curva. Não há sobreposição quando esses retângulos são transladados horizontalmente para R .

Passo 1

Então galera, primeiramente devemos determinar quem são as somas superiores e quem são as somas inferiores, ok? As partições relacionadas ao máximo, que iremos chamar de U , será:

U = m a x 1 ∆ x + m a x 2 ∆ x + …   + m a x n ∆ x

Mas po, quem são esses máximos aí? Esses máximos são os valores que a função apresenta no pontos de x , isto é:

m a x 1 = f x 1 ,   m a x 2 = f x 2 , …   , m a x n = f ( x n )  

Passo 2

Agora temos que determinar as partições relacionadas ao mínimo, certo? Esse mínimo chamaremos de L , ok? Fazendo a mesma coisa que fizemos no passo anterior, teremos:

L = m i n 1 ∆ x + m i n 2 ∆ x + …   + m i n n ∆ x

Mas quem são esses mínimos aí? De acordo com o gráfico, esses são os valores que a função apresenta nos pontos de x também, mas com uma diferença:

m i n 1 = f x 0 ,   m i n 2 = f x 1 , …   , m i n n = f ( x n - 1 )

Passo 3

Agora que determinarmos as somas superiores e inferiores, basta fazermos a diferença entre ambos ( U - L ) , assim como a questão solicita, beleza? Fazendo isso então, teremos:

U - L = m a x 1 - m i n 1 ∆ x + m a x 2 - m i n 2 ∆ x ,   …   , m a x n - m i n n ∆ x

U - L = f x 1 - f x 0 ∆ x + f x 2 - f x 1 ∆ x , …   , f x n - f x n - 1 ∆ x

Se fizéssemos isso para todos os pontos, notaríamos que sobraria o seguinte:

U - L = f x n - f x 0 ∆ x

E como, de acordo com o gráfico, x n = b e x 0 = a , então:

∴ U - L = f b - f a ∆ x

CQD.

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Seja f : 0,1 → R dada por f ( x ) = 0s ex∉0 , 1 2 , 11s ex∈0 , 1 2 , 1 Prove que f é integrável em [ 0,1 ] e que ∫ 0 1 f ( x ) d x = 0
Seja f : 0,1 → R dada por f ( x ) = xs ex∈Q0s ex∉Q Verifique que se os c i forem racionais ∑ i = 1 n f c i △ x i tende a 1 2 , quando m a x△ x→ 0 .Prove que f não é integrável em 0,1 .
38. Prove que a função maior inteiro é descontínua em [ 0 , 3 2 ] e mesmo assim é integrável nesse intervalo. Mostre também que ∫ 0 3 / 2 x d x = 1 2
37. Prove que a função sinal é descontínua em [ - 1,1 ] e mesmo assim é integrável nesse intervalo. Mostre também que ∫ - 1 1 s g n xd x = 0
Expresse como uma integral definida: lim n → + ∞ ⁡ ∑ i = 1 n n i + n 2 Sugestão: considere a fução f para a qual f x = 1 x 2 em [ 1,2 ] .