Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 11.2 - Ex. 11
9-14. Calcule pelo menos dez somas parciais da série. Faça o gráfico de ambas as sequências de termos e de somas parciais na mesma tela. Parece que a série é convergente ou divergente? Se ela for convergente, calcule a soma. Se for divergente, explique por quê.
11.
Passo 1
Então pessoal, a questão nos pede várias coisas, então vamos tratar a questão com calma, passo a passo, ok? De início, o enunciado nos pede para calcular pelo menos dez somas parciais da série. Para calcularmos essas somas parciais, devemos fazer:
Mas o que seriam esses termos? De forma genérica, temos que uma série é descrita da seguinte forma:
No qual é sua n-ésima soma parcial e é a sequência de termos. No nosso caso, temos:
Passo 2
Botando em prática o conceito abordado no passo anterior, teremos:
Passo 3
Ok, agora que descobrimos as dez somas parciais da série, basta plotarmos esses pontos em um gráfico juntamente com a sequência de termos, assim como o enunciado solicita. Se fizermos isso, obteremos o seguinte resultado:
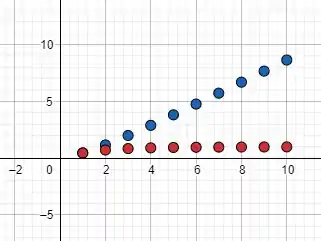
No qual os pontos em azul são referentes às somas parciais da série e os pontos em vermelho são referentes aos valores da sequência de termos. Pelo gráfico podemos notar que os pontos da sequência de termos não se aproximam de , o que é um indicativo de que a série é divergente. Ademais, os pontos das somas parciais não tendem a nenhum valor específico, que é mais um indicativo de que a série é divergente. Mas po, como faço para provar que é divergente ou não? Utilizemos o teste da divergência, que nos diz o seguinte:
“Se ou se , então a série é divergente.”
Se esses limites não derem isso, então a mesma será convergente. Fazendo o teste:
Dividindo todos os termos por , teremos:
Aplicando o limite:
Sendo assim, a conclusão que tiramos é de que a série é divergente, assim como esperávamos!