Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 10.Revisão - Ex. 46

Ache a área de intersecção das regiões limitadas pelos gráficos das duas equações r = a c o s θ e r = a ( 1 - c o s θ ) , a > 0.

Passo 1

Para entender melhor a questão é bom ter um ideia de com é o gráficos das equações:

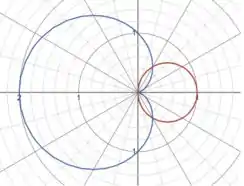
Note que, a área da região de a questão se refere pode ser dividida em duas iguais, desse modo facilita o cálculo.

Passo 2

Com isso, o primeiro passo é encontro o ângulo de intersecção, para isso basta igualar as duas equações:

a c o s θ = a ( 1 - c o s θ )

2 c o s θ = 1

c o s θ = 1 2

Com queremos o ângulo apena no primeiro quadrante, então arc cos é π / 3 .

Desse modo, a região é dividida em duas a primeira indo de 0 a π 3 e a outra de π 3   a π 2 .

Passo 3

Portando, e sabendo que a área da região é dada por:

A = 1 2 ∫ α β   f θ 2   d θ

A = ∫ 0 π / 3 a - a c o s θ 2 d θ + ∫ π 3 π 2 a c o s θ 2 d θ

A = a ² ∫ 0 π / 3 1 - 2 c o s θ + c o s ² θ   d θ + a ² ∫ π 3 π 2 c o s ² θ   d θ

Aplicando as propriedades trigonométricas, temos:

A = a 2 θ - 2 s e n θ + 1 2 θ + s e n 2 θ 2 |   0 π 3 + a 2 1 2 θ + s e n 2 θ 2 |   π 3 π 2

A = 0.10 a ²

Resposta

0.10a²

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Nos exercícios 9 a 32 esboçar o gráfico das curvas dadas em coordenadas polares.
Nos exercícios 33 a 37 , encontrar o comprimento de arco da curva dada.
Nos exercícios 33 a 3 7 , encontrar o comprimento de arco da curva dada.
Achar o comprimento da cardioide r = 10 (1 - c o s theta)
Nos exercícios de 39 a 46 , encontrar a integral que dá o comprimento total da curva dada.