Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 10.Revisão - Ex. 33b
Faça um esboço do gráfico de:
Passo 1
A princípio parece bem estranho né? Mas vamos digerir essa equação com calma. A gente ta trabalhando com uma coisa chamada espiral de Arquimedes. Ela sempre começa da origem e vai crescendo simetricamente em x e y. Essa espiral segue algumas regras que vamos usar para o nosso esboço. Ela sempre segue a regra de:
Seu diâmetro de separação corresponde a:
Passo 2
Logo, vamos ao desenho... Cuidado para não hipnotizar!
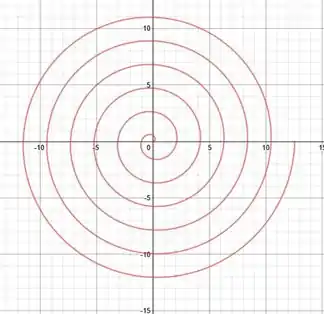
Resposta
Exercícios de Livros Relacionados
As coordenadas cartesianas de um ponto são dadas. (i) Encontre as coordenadas polares ( r ,θ ) do ponto, onde r0 e 0 ≤ θ2 π .(ii) Encontre as coordenadas polares ( r ,θ ) do ponto, onde r0 e 0 ≤ θ2 π
Plote o ponto cujas coordenadas polares são dadas. Então encontre as coordendas cartesianas do ponto.a) 3 , π 2 b) 2 2 ,3 π 4 c) - 1 ,π 3
Plote o ponto cujas coordenadas polares são dadas. Então encontre dois outros pares de coordenadas polares desse ponto com r0 e outro com r0 .a) 1 , π 2 b) - 2 , π 4 c) 3 ,2
Plote o ponto cujas coordenadas polares são dadas. Então encontre dois outros pares de coordenadas polares desse ponto com r0 e outro com r0 .a) 3 ,0 b) 2 ,- π 7 c) - 1 ,- π 2
Encontre uma equação polar para a curva representada pela equação cartesiana dada. x + y = 9