Enunciado
Cálculo - Diva Flemming - Cálculo A- Ed: 6º - Capítulo 8.11 - Ex. 23
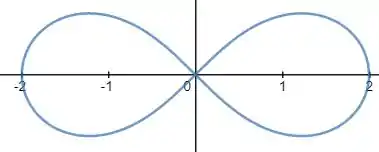
Nos exercícios a esboçar o gráfico das curvas dadas em coordenadas polares.
Passo 1
Para este exercício, a equação pode ser reescrita como:
Com isso, deve-se lembrar que esta equação representa o gráfico de uma lemniscata que possui uma equação da forma:
Além disso, pode-se concluir que a curva é simétrica em relação ao eixo , pois:
E também é simétrica em relação ao eixo , pelo fato de que:
Dessa forma, torna-se possível fazer a análise no intervalo .
Passo 2
Assim, os pontos do gráfico serão analisados por uma tabela que dará o valor de a partir de cada valor de . Então:
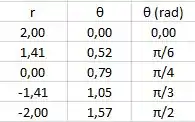
Passo 3
Analisando a tabela e os dados pontos, o gráfico da equação será dado por:
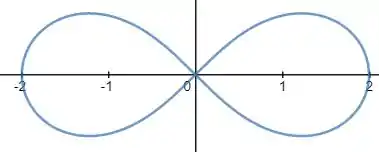
Resposta
Exercícios de Livros Relacionados
Encontre equações polares para os círculos nos Exercícios 33-36. Esboce cada círculo no plano coordenado e rotule-o com suas equações cartesianas e polares. x 2 + y 2 - 2 y = 0
Esboce as retas nos Exercícios 23-28. Determine também uma equação cartesiana para cada reta. r = 2 sec θ
Esboce as retas nos Exercícios 23-28. Determine também uma equação cartesiana para cada reta. r c o s θ + π 3 = 2 3
Esboce as retas nos Exercícios 23-28. Determine também uma equação cartesiana para cada reta. r = - 2 sec θ
Encontre equações cartesianas para os círculos nos Exercícios 29-32. Esboce cada círculo no plano coordenado e rotule-o com as equações cartesianas e polares. r = - 6 cos θ