Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 4.2 - Ex. 9
Ache a área do maior retângulo tendo 2 vértices no eixo e os dois outros vértices sobre a parábola acima do eixo .
Passo 1
Essas questões têm um jeito bem metódico de resolver, saca só:
- Precisamos de uma equação que associe a variável que queremos maximizar e outra variável do problema. Essa é normalmente a parte mais difícil do problema.
- Depois que temos essa função, vamos encontrar a derivada dela e procurar os valores onde ela se iguala a e os valores onde ela não existe.
- A partir do Teorema do Valor Extremo vamos encontrar os máximos e mínimos comparando os valores da função original nos extremos do intervalo e nos pontos onde a derivada é nula ou inexistente.
Passo 2
Vamos começar desenhando que clareia tudo na nossa mente. Temos a parábola indicada:
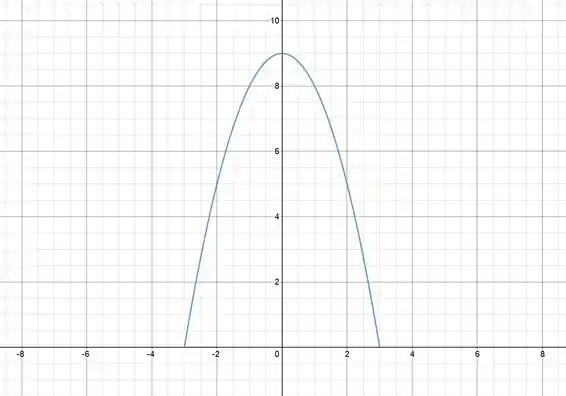
O problema quer o retângulo com 2 vértices no eixo e outros dois na parábola. Mais ou menos assim:
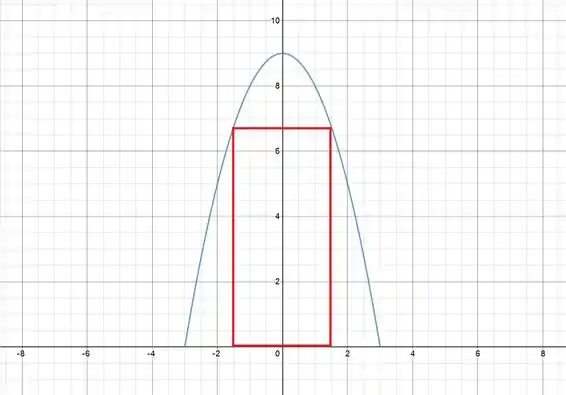
Daí já vemos que o nosso domínio será . Mas vamos considerar o valor da distancia entre a origem e o ponto do vértice sobre o eixo. Daí ficamos com .
Passo 3
Agora que temos uma ideia melhor do que tá acontecendo, vamos equacionar as coisas. Queremos a área desse retângulo, que é dada por:
Estamos usando pois representa metade de uma das base do retângulo. E a nossa outra restrição é essa parábola:
Então podemos substituir isso na equação da área e ficar com uma variável só:
Agora é só derivar essa belezinha e encontrar o seu valor máximo!
Passo 4
Derivando
Igualando a
Como queremos valores positivos de :
Então o tamanho da base do retângulo será !
Passo 5
Para achar o valor de sua altura é só substituir o valor de que encontramos na equação da parábola:
Então o nosso retângulo tem base e altura . Sua área será: