Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 4.Revisão - Ex. 89
Sejam e duas funções diferenciáveis em todo número no intervalo fechado [a,b]. Suponha, então, que e . Prove que existe um número c no intervalo aberto (a,b); tal que . (Sugestão: considere a função .)
Passo 1
Primeiro imaginamos duas funções que obedecem ao que o texto mencionou. Por exemplo, se e .
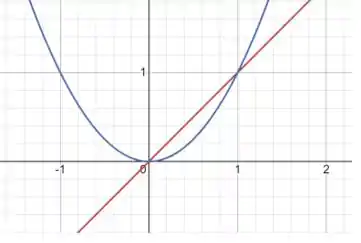
Note que, existem dois ponto na qual, e , que neste caso são os ponto x=0 e x=1. Para isso, vamos criar uma função onde onde se os pontos corresponderem ao mesmo valor é 0, e a derivada, vai existir no intervalo (a,b)
Passo 2
Obeserve que, pelo menos uma das funções tem quer ter grau maior ou igual a 2, pois se as duas funções forem lineares não vai existir dois ponto na qual se cruzem, como também uma das fuções tem que ter um grau maior que a outra.
Desse modo, suponhamos duas funções genéricas:
Onde, a>0, b>0, c>0 e b>d.
Com isso, temos:
Passo 3
Dessa maneira, vamos verificar os pontos de igualdade.
Agora basta derivarmos h, e igualarmos a 0.
Note que, , desse modo, existe um número c pertencente ao intervalo aberto (a,b) tal que .
Resposta
Ei, a resposta está no passo a passo :)