Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 9.Revisão - Ex. 98

Ache a área da região limitada pela curva y = a r c s e n   2 x , pela reta x = 1 4 3 e pelo eixo x .

Passo 1

O exercício pede para calcularmos a área da região delimitada pelas curvas y = a r c s e n   2 x , x = 1 4 3 e o eixo x ( y = 0 ). Como é difícil trabalhar com a função arco seno, a dica aqui é inverter a primeira curva:

y = a r c s e n   2 x ⇒ 2 x = s e n   y ⇒ x = 1 2 s e n   y

Plotando essas curvas em um gráfico, temos que

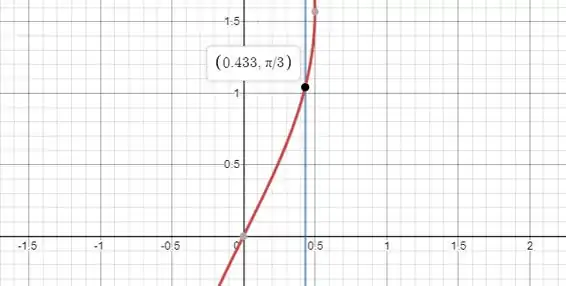
O ponto de interseção é encontrado fazendo

1 2 s e n   y = 1 4 3 ⇒ s e n   y = 3 2 ⇒ y = π 3

Fazendo a integração na direção x , teríamos:

A = ∫ 0 1 4 3 a r c s e n   2 x   d x

Essa é uma integral chata e pouco usual, então vamos ver o que acontece se escrevermos a integral na direção y :

A = ∫ 0 π / 3 1 4 3 - 1 2 s e n   y   d y

Note que fixando a variável de integração, a região de interesse vai da curva x = 1 2   s e n   y até a reta x = 1 4 3 , por isso a integral tem essa cara. Além disso, a função seno é bem fácil de ser integrada!

Passo 2

Efetuando a integral, temos que

A = 3 4 y + 1 2 cos ⁡ y 0 π / 3 = 3 4 π 3 - 0 + 1 2 cos ⁡ π 3 - cos ⁡ 0

Assim,

A = π 3 12 + 1 2 1 2 - 1

Portanto, a área será

A = π 3 12 - 1 4

Resposta

π 3 12 - 1 4

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Encontre o comprimento exato da curva. y = 1 4 x 2 - 1 2 ln ⁡ x , 1 ≤ x ≤ 2
Encontre o comprimento exato da curva. y = ln ⁡ ( 1 - x 2 ) , 0 ≤ x ≤ 1 2
Encontre o comprimento exato da curva. y = 1 - e - x , 0 ≤ x ≤ 2
Escreva uma integral para o comprimento da curva. Use sua calculadora para encontrar o comprimento da curva com precisão de quatro casas decimais. y = x e - x ,0 ≤ x ≤ 2
Trace a curva estime visualmente seu comprimento. Use sua calculadora para encontrar o comprimento da curva com precisão de quatro casas decimais. y = x 2 + x 3 ,1 ≤ x ≤ 2