Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 9.3 - Ex. 37

Ache a área da região limitada pela curva y = t g ²   x , pelo eixo x e pela reta x = 1 4 π .

Passo 1

Para começar, desenhamos a situação descrita pelo problema:

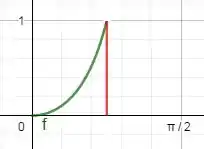
Para achar a área abaixo da curva delimitada entre 0 < x < 1 4 π , devemos integrar a função nestes limites:

∫ 0 π 4 t g ² ( x ) . d x

Lembrando que:

t g ² ( x ) = s e c ² ( x ) - 1

Então

∫ 0 π 4 t g ² ( x ) . d x = ∫ 0 π 4 s e c ² ( x ) - 1 . d x = ∫ 0 π 4 s e c ² ( x ) . d x - ∫ 0 π 4 d x = t g   x π 4 0 - x π 4 0 = t g   π 4 - t g   0 - π 4 - 0 = 1 + π 4

Resposta

Á r e a = 1 + π 4

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Nos exercícios de 15 a 36, calcule a integral indefinida. (36) ∫ c o t g ( t ) t d t
Prove o teorema 7.4.6 tomando ∫ c o s e c u d u = ∫ sec ⁡ u - π 2 d u e usando o teorema 7.4.5 e as identidades trigonométricas.
Nos Exercícios de 1 a 30, calcule a integral indefinida. 21 )∫ 2 . s e nw - 1 cos ² ⁡ w . d w ²
Nos Exercícios de 1 a 30, calcule a integral indefinida. 20 )∫ d x 1 + cos ⁡ x
Nos Exercícios de 1 a 30, calcule a integral indefinida. 22 )∫ t g ³x x . d x ³