Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 7.6 - Ex. 52
Ache a área da região limitada pelos gráficos de e pelas retas e .
Passo 1
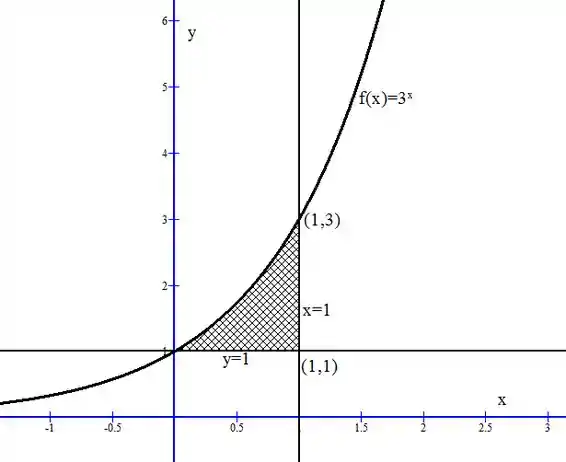
O primeiro passo para o cálculo da área de uma região é fazer um esboço. A função parte do ponto e cresce até , onde toca na reta . Essa região ainda é limitada por baixo pela reta horizontal . A região então fica assim:
Passo 2
Agora calculamos a integral definida, no intervalo :
Sabendo que :
Resposta
Exercícios de Livros Relacionados
Quantidade ideal de pedidos Uma das fórmulas para gerenciamento de estoque diz que o custo médio semanal de pedidos, pagamentos e armazenamento de mercadoria é A q = k m q + e m + h q 2 em que q é a q
Uma empresa estima que em t anos o número de seus empregados será N t = 1000 0,8 t 2 a ) Quantos empregados a empresa espera ter em 4 anos? b ) Com que taxa estará variando o número em 4 anos?
Uma empresa determinou que ao iniciar uma nova promoção de vendas, o número de vendas por dia aumenta. No entanto, o número diário de vendas adicionais decresce quando o impacto da promoção se desgast
Uma partícula move-se ao longo de uma reta, de acordo com a equação do movimento s = A ∙ 2 k t + B ∙ 2 - k t , onde A , B e k são constantes e s m é a distância orientada da partícula a partir da orig
Prove que D x n ln x = - 1 n - 1 n - 1 ! x n Sugestão: Use indução matemática.