Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 10.3 - Ex. 8

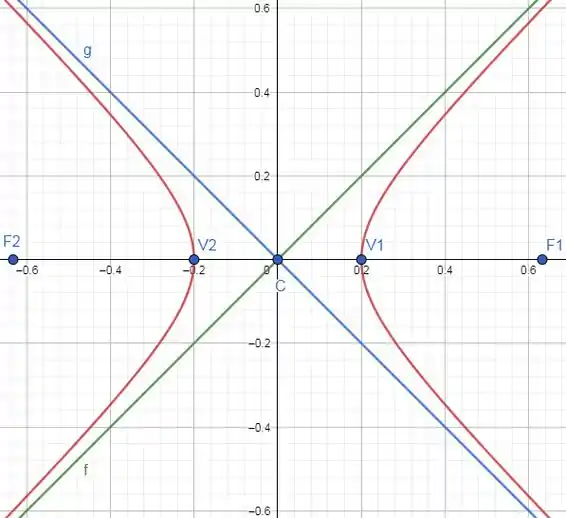
Ache o centro, os vértices, os focos e as equações das assíntotas da hipérbole dada. Faça um esboço da curva e de suas assíntotas e mostre os focos.

25 x 2 - 25 y 2 = 1

Passo 1

Primeiramente vamos passar a equação para a forma reduzida.

x 2 1 25 - y 2 1 25 = 1

Desta forma temos que o centro é 0 ,   0 , pois não há termo somando ou subtraindo de x e y . Além disso a 2 = b 2 = 1 25 que nos dão os valores dos eixos a = b = 5 .

Passo 2

Agora para achar os vértices tomamos o centro e somamos ou subtraímos a da coordenada da qual o eixo principal é paralelo. Neste caso temos que fazer isso em x .

V 1 = 0 + 1 5 ,   0

V 1 = 1 5 ,   0

V 2 = 0 - 1 5 ,   0

V 2 = - 1 5 ,   0

Passo 3

Para os focos o mesmo procedimento dos vértices pode ser aplicado, mas em relação a c . Assim basta encontrar c   pela Relação Pitagórica.

a 2 + b 2 = c 2

1 25 + 1 25 = c 2

2 5 = c

F 1 = 0 + 2 5 ,   0

F 1 = 2 5 ,   0

F 2 = 0 - 2 5 ,   0

F 2 = - 2 5 ,   0

Passo 4

As assíntotas são dadas como f x = b a x e g x =   - b a x

f x = 1 5 1 5 x

f x = x

g x =   - 1 5 1 5 x

g x =   - x

Resposta

C = 0 ,   0

V 1 = 1 5 ,   0

V 2 = - 1 5 ,   0

F 1 = 2 5 ,   0

F 2 = - 2 5 ,   0

f x = x

g x =   - x

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Ache a equação da hipérbole satisfazendo as condições dadas e faça um esboço do gráfico.Focos em ( 0,5 ) e ( 0 ,- 5 ) e um vértice ( 0 ,4 ) .
Ache a equação da hipérbole satisfazendo as condições dadas e faça um esboço do gráfico.Vértices em ( - 2,0 ) e ( 2 ,0 ) e um eixo conjugado com comprimento 6.
Ache a equação da hipérbole satisfazendo as condições dadas e faça um esboço do gráfico.Centro na origem, focos sobre o eixoy e passando pelos pontos ( - 2 ,4 ) e ( - 6 ,7 ) .
Ache a equação da hipérbole satisfazendo as condições dadas e faça um esboço do gráfico.Centro em 3 ,- 5 , um vértice em 7 ,- 5 e um foco 8 ,- 5 .
Ache a equação da hipérbole satisfazendo as condições dadas e faça um esboço do gráfico.Extremidade do eixo conjugado em ( 0 ,- 3 ) e 0 ,3 e um foco em 5 ,0 .