Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 9.2 - Ex. 46
Ache o centroide da regiãodescrita no Exercício 44.
Passo 1
A região do exercício 44, é dada pelas curvas e para. Vamos esboçar a região para visualizarmos melhor:
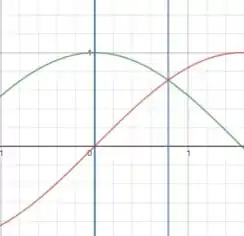
Como dá para ver, a função cosseno (linha vermelha) está acima da função seno (linha verde) na região de nosso interesse e para integrarmos essa região para obtermos o centroide, precisaremos fazer a diferença entre as funções:
Precisaremos então determinar os valores dos momentos de massa , e a área A da região para podermos calcular o centroide, as equações então serão:
Passo 2
Vamos primeiro resolver a equação da área da região:
Integrando cada termo:
Aplicando os limites:
Passo 3
Para resolvermos , vamos expandir a potência:
E podemos escrever:
Transformando a integral em uma integral indefinida e fazendo a substituição :
Integrando:
Retornando para a variável x:
E substituindo os limites de integração:
Passo 4
Para calcularmos usaremos o método de integração por partes:
Chamaremos e . A integral então fica:
Integrando cada termo da ultima integral:
Aplicando os limites:
Passo 5
E agora jogamos os resultados nas equações das coordenadas do centroide:
E então o centroide terá aproximadamente as coordenadas (0,27, 0,60)
Resposta
(0,27, 0,60)