Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 9.Revisão - Ex. 105

Ache o centroide da região do exercício 99.

Passo 1

A questão pede para você determinar o centroide da região do exercício 99. No exercício 99, calcularmos a área da região delimitada pelo laço x^2 = y^4 ( 1 - y^2 ) , indicado na figura a seguir:

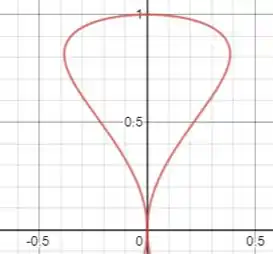
Neste exercício, vimos que a integração é feita de forma mais simples na variável y e obtivemos A = pi // 8 para a área.

Note que a região é simétrica com relação ao eixo y , de modo que a coordenada overset(-)(x) do centroide será nula:

overset(-)(x) = 0

Já para a coordenada y do centroide, temos que

overset(-)(y) = (M_x)/(M) ,

onde

M = k A e M_x = 2 k int_0^1 x y d y

Usei essa expressão para M_x pois a integral é feita na variável y . O fator 2 aparece porque a integral só considera a região do primeiro quadrante.

Como x^2 = y^4 ( 1 - y^2 ) , temos que no primeiro quadrante x = y^2 sqrt(1 - y^2) . Assim,

M_x = 2 k int_0^1 y^2 sqrt(1 - y^2) y d y

Passo 2

Chamando t = 1 - y^2 , temos que d t = - 2 y d y . Além disso, y^2 = 1 - t e quando y = 0 , t = 1 , enquanto para y = 1 , temos t = 0 :

M_x = - k int_1^0 (1 - t) sqrt(t) d t = k int_0^1 (t^((1)/(2)) - t^((3)/(2))) d t

Fazendo a integral:

M_x = k ((2)/(3) t^((3)/(2)) - (2)/(5) t^((5)/(2)))_0^1 = k ((2)/(3) - (2)/(5)) = (k (10 - 6))/(15) = (4 k)/(15)

Passo 3

Assim,

overset(-)(y) = (M_x)/(M) = ((4 k)/(15))/((k pi)/(8)) = (32)/(15 pi)

Portanto, as coordenadas do centroide serão:

(overset(-)(x) , overset(-)(y)) = (0 , (32)/(15 pi))

Resposta

(0 , (32)/(15 pi))

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Suponha que a velocidade de uma formiga correndo ao longo da beirada de um muro seja modelada pela função v t =5 t , 0 ≤ t1 6 t - 1 t , 1 ≤ t ≤ 2 onde t está em segundos e v está em centímetros por se
Suponha que a função velocidade uma partícula em movimento retilíneo ao longo de um eixo s seja v t = 20 t 2 - 110 t + 120m / s e que a partícula esteja no instante t = 0 .Use um recurso gráfico para
Determine se a afirmação dada é verdadeira ou falsa. Explique sua resposta. Cada afirmação se refere a uma partícula em movimento retilíneo.Se a partícula tiver aceleração constante não nula, então o
Suponha que a velocidade de um camundongo correndo ao longo do rodapé de um quarto seja modelada pela função v t = 3 t 2 + 1 - 0,5 t,0 ≤ t ≤ 6 onde t está em segundos e v está em metros por segundo (m
Suponha que a função aceleração de uma partícula em movimento retilíneo ao longo de um eixo s seja a t = 4 t - 30m / s 2 e que a posição e a velocidade no instante t = 0 sejam s 0 = - 5 m e v 0 = 3m /