Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 6.Revisão - Ex. 29
Ache o centróide da região limitada pela parábola e pela reta .
Passo 1
A primeira coisa a se fazer aqui, pessoal, é tentar indentificar que região é essa, no nosso caso, temos uma parábola com concavidade para cima e vértice na origem e a função . Em um gráfico, ficamos com o seguinte:
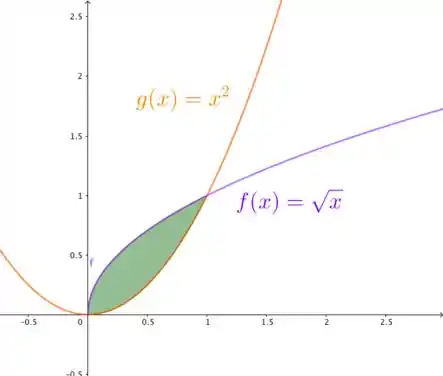
Percebam que a parábola e a reta passam pelos pontos e , logo, esses são os pontos de interseção.
É importante perceber que aqui nós vamos usar integrais em relação a , para achar o centróide e também que a região é limitada por duas curvas.
Vamos lembrar a fórmula do centróide: Seja a região limitada pelas curvas e , pelas retas e . A função é contínua em e . Se denotar o momento de em relação ao eixo e denotar o momento de em relação ao eixo , então:
E se for o centróide da região plana cuja área é unidades quadradas e e forem definidos como acima, temos:
Pronto! Agora devemos achar e . Sendo e . Lembre-se: é a função maior e a menor.
Passo 2
Vamos começar achando a área da região no intervalo de (lembre-se dos pontos de interseção do gráfico). Sendo assim, a área será dada pela seguinte integral definida:
Lembre-se que .
Passo 3
Agora acharemos o momento da região em relação ao eixo .
Passo 4
Agora acharemos o momento da região em relação ao eixo .
Passo 5
Por último vamos substituir tudo na fórmula do centróide:
Prontinho, achamos o centróide.