Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 4.2 - Ex. 24
Ache as dimensões do cilindro circular reto de maior volume que possa ser inscrito em uma esfera com raio de cm.
Passo 1
Essas questões têm um jeito bem metódico de resolver, saca só:
- Precisamos de uma equação que associe a variável que queremos maximizar e outra variável do problema. Essa é normalmente a parte mais difícil do problema.
- Depois que temos essa função, vamos encontrar a derivada dela e procurar os valores onde ela se iguala a e os valores onde ela não existe.
- A partir do Teorema do Valor Extremo vamos encontrar os máximos e mínimos comparando os valores da função original nos extremos do intervalo e nos pontos onde a derivada é nula ou inexistente.
Passo 2
A ideia dessa questão é parecida com a anterior, mas dessa vez não queremos maximizar a área lateral, mas sim o volume do cilindro. Vamos usar os mesmos parâmetros que usamos lá pra ficar bem análogo.
Imagine um cilindro inscrito em uma esfera de raio . Agora imagine que é o ângulo entre o eixo central do cilindro e o ponto superior de interseção entre o cilindro e a esfera. Daí já podemos restringir no conjunto :
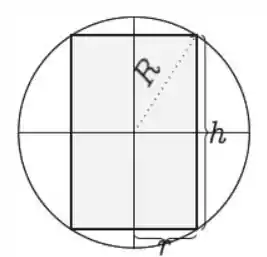
Então o raio desse cilindro será:
E sua altura será:
Agora vamos definir a equação do volume do cilindro:
Substituindo os valores de e
Agora vamos derivar e igualar a e encontraremos o nosso ponto de máximo!
Passo 3
Derivando :
E se precisarmos achar onde a derivada é nula, teremos que:
Dividindo tudo por
Lembre-se que
Então:
Agora é só substituir o valor de e nas equações para a altura e para o raio do cilindro e acabamos!
Passo 4
Resposta
O raio é cm, a altura é cm.