Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 2.7 - Ex. 20
Ache o domínio da função e diga se é contínua nos intervalos:
Intervalos:
Passo 1
Antes de determinarmos o domínio dessa função, vamos lembrar o que significa a notação
Essa notação representa a função ‘piso’, que retorna o maior inteiro que é menor ou igual a x.
Assim, para valores de x positivos, equivale a pegar apenas a parte inteira do número, como por exemplo
Para valores negativos, se for fracionário, pega-se a parte inteira e subtrai 1, se for inteiro é o próprio número, como por exemplo .
Assim, como podemos calcular a parte inteira de qualquer número, não temos restrições e nosso domínio é (todos os reais)
Passo 2
Para determinar a continuidade em cada intervalo, sabemos que não temos restrições mas sim saltos, pois essa função é a famosa ‘função escada’, como nesse exemplo:
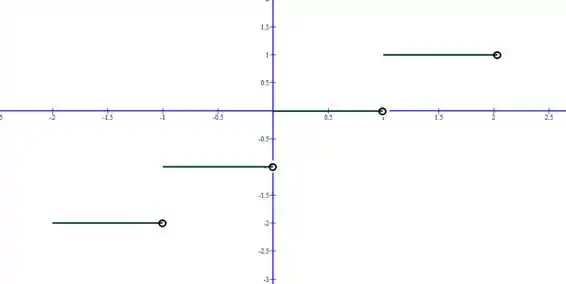
Repare que qualquer intervalo que esteja contido entre dois inteiros sucessivos é contínuo, pois possuem a mesma parte inteira, como por exemplo , onde todos possuem a mesma parte inteira 0.
Assim, o possível problema para a continuidade vai estar exatamente nos intervalos que contém números inteiros, que podem ou não ser contínuos.
Pensa na escada: dentro dos degrais, temos uma reta constante (contínuo), mas no pulo de um degrau para o outro, temos descontinuidades!
Assim, vamos analisar os intervalos da seguinte forma: se todos tiverem entre dois inteiros sucessivos, então é contínuo. Se houver inteiros dentro do intervalo, então é descontínuo. Se os extremos forem inteiros, analisaremos cada caso.
Passo 3
Intervalo : como o inteiro 0 está dentro dele, é descontínuo.
Intervalo : como não há inteiros dentro dele, é contínuo.
Intervalo : como os inteiros não estão inclusos, é contínuo.
Intervalo : a parte inteira de 1 é 1 e dos demais valores 1,... também é 1, então é contínua
Intervalo : a parte inteira de valores 1,... é 1, mas ao saltar para o 2, a parte inteira é 2, então há um salto (como pode ver no gráfico), então é descontínua.
Resposta
É contínua nos intervalos:
Não é contínua nos intervalos: :