Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 2.10 - Ex. 9
Uma função é dada.
a) Determine os valores de tais que .
b) Ache todos os intervalos abertos contendo um valor particular de que satisfaçam a parte a) tais que para todo em .
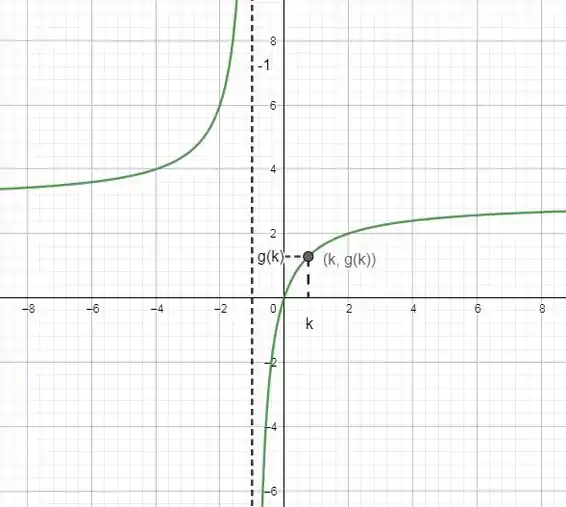
c) Faça um esboço do gráfico de e mostre no gráfico a interpretação geométrica dos resultados das partes a) e b).
Passo 1
a)
Aplicando o caso 1 temos que
Assim o conjunto solução deste caso é
Aplicando o caso 2 temos que
Assim o conjunto solução deste caso é
Então sempre que estiver nos intervalos e
Resposta
a) sempre que estiver nos intervalos e
b) Como > 0, somente se ou , os intervalos abertos requeridos contendo k e tais que > 0 são aqueles para os quais e ou e .
c)
Exercícios de Livros Relacionados
Determine, se existirem, os valores de x ∈ D f , nos quais a função f x não é contínua. f x = 1 + cos x 3 + sen x
Investigue a continuidade nos pontos indicados: f x = 1 sen 1 xe mx = 2
Investigue a continuidade nos pontos indicados: f x = x - xe mx = 0
Investigue a continuidade nos pontos indicados: f x = 1 - x 2 ,x1 1 - x ,x1 1 ,x = 1e mx = 1
Investigue a continuidade nos pontos indicados: f x = x 3 - 8 x 2 - 4 ,x ≠ 2 3 ,x = 2e mx = 2