Enunciado
Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 22.Exercício - Ex. 87
Prove que qualquer reta tangente a uma hipérbole separa os focos.
Passo 1
Considerando uma equação de hipérbole igual a
E considerando a equação de tangente igual a:
E considerando os focos em posições iguais a:
Em a equação da reta tangente terá um igual a:
E queremos provar se esse valor de está com um valor entre o valor de dos focos.
Passo 2
E por termos uma hipérbole então:
Como queremos saber se a posição está entre e então teremos que observar que então:
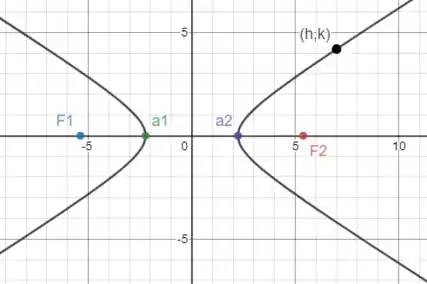
O valor de por ser um ponto de tangência horizontal então certamente , logo
E como , logo obrigatoriamente , portanto para qualquer reta tangente a hipérbole (que segue a equação de tangência dada no passo 1) a reta cortará os focos
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Determinar uma equação da hipérbole que satisfaça as condições dadas. Esboçar o gráfico.Vértices A 0 , ± 2 , distância focal 2 11
Determinar uma equação da hipérbole que satisfaça as condições dadas. Esboçar o gráfico.Vértice em 3 , - 2 e 5 , - 2 e um foco em 7 , - 2
Determinar uma equação da hipérbole que satisfaça as condições dadas. Esboçar o gráfico.Focos F 1 3 , - 2 e F 2 3,4 e excentricidade 2
Determinar uma equação da hipérbole que satisfaça as condições dadas. Esboçar o gráfico.Vértices A ± 3,0 e equações das assíntotas y = ± 2 x
Determinar uma equação da hipérbole que satisfaça as condições dadas. Esboçar o gráfico.Vértices A 0 , ± 2 e equações das assíntotas y = ± 1 4 x