Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 3.6 - Ex. 37
Ache uma equação da reta tangente à curva em cada um dos seguintes pontos . Faça um esboço do gráfico e desenhe segmentos das retas tangentes nos pontos dados.
Passo 1
Bom, o exercício pede para a gente calcular retas tangentes a uma determinada função, então vamos precisar fazer a derivada da função para encontrarmos as inclinações de cada um dos segmentos.
Passo 2
Para fazer a derivada de y, vamos precisar usar a Regra da Cadeia. Primeiro derivamos a função de fora, que no caso é o quadrado de fora:
Colocamos a função de dentro no lugar de t e depois multiplicamos pela derivada dessa função:
Resolvendo a última derivada que apareceu e o produto:
Passo 3
Agora para cada ponto dado no enunciado, vamos substituir o valor de x para termos o valor da inclinação de cada reta, que chamaremos de T,
Para :
Para :
Para :
Para :
E para :
Passo 4
Bom, agora que já temos as inclinações, basta substituir elas na equação da reta para cada ponto, onde e são as coordenadas de cada ponto, que o enunciado já nos deu:
Para :
Para :
Para :
Para :
E para :
Passo 5
E os segmentos ficarão da seguinte maneira no gráfico na função:
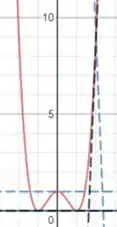
Resposta
Ei, a resposta está no passo a passo :)