Enunciado

Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 4.8 - Ex. 2

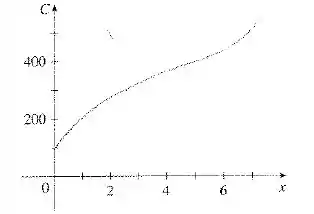
É dado o gráfico da função custo.

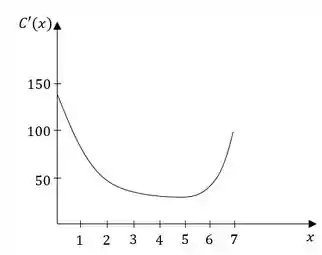
Faça um esboço cuidadoso da função custo marginal.

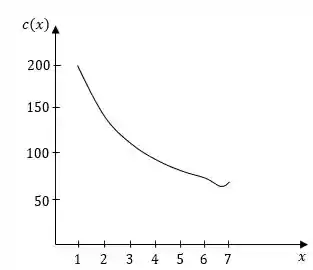
Use a interpretação geométrica do custo médio como uma inclinação (veja a figura 1) para fazer um esboço cuidadoso da função custo médio.

Estime o valor de para o qual é um mínimo. Como estão relacionados os custos médio e marginal naquele valor de ?

Passo 1

Olá, meu amigo. Vou te ajudar a resolver mais uma atividade hoje.

Temos o gráfico da função , que representa o custo.

E precisamos encontrar algumas informações sobre ele. Precisamos de inicio esboçar a função custo marginal, dado esse gráfico. O custo marginal é dado por , isso significa que deveremos traçar retas tangentes em diferentes ponto do gráfico, devemos então aproximar o valor dessas inclinações para que possamos então construir o gráfico.

A função custo médio é cada por:

Devemos então aproximar diversos pontos no gráfico do custo para conseguirmos resolver essa.

Passo 2

Para esboçar o gráfico do custo marginal temos que traçar as tangentes à curva em cada ponto e analizar as inclinações em relação à horizontal. Transferindo as retas tangentes para a origem, podemos avaliar seu valor, que é numerivamente igual à tangente do ângulo em relação à horizontal.

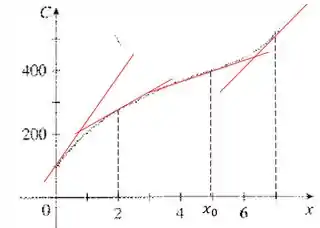
A inclinação em é aproximadamente igual a , depois em aproximadamente igual a .

Depois passa por um ponto de inclinação mínima aproximadamente igual a em e no final volta a aumentar até em . Esboçando, temos a seguinte curva:

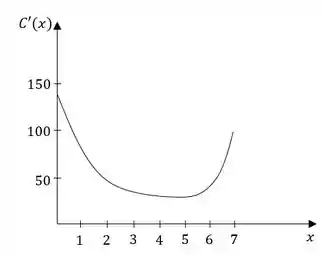
Passo 3

Para traçar a curva do custo médio , vamos ligar os pontos da curva à origem e calcular as tangentes dos ângulos entre as retas e a horizontal.

Vamos fazer isso para . Para ilustrar, fazemos só a reta para , em vermelho.

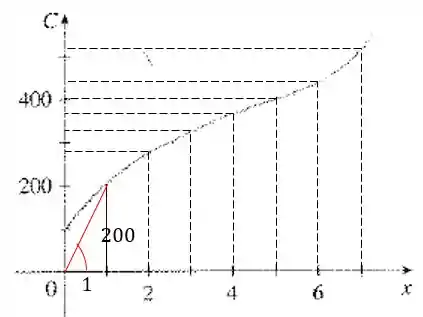
Então temos:

Com isso esboçamos a função . Devemos notar que o ponto mínimo de ocorre entre e .

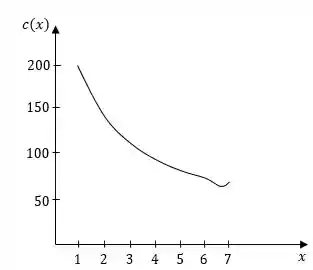
Passo 4

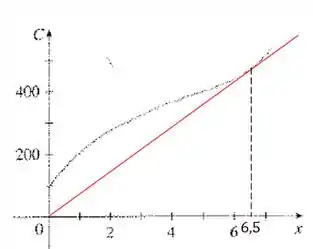
será mínimo quando a reta que liga um ponto da curva à origem for menos inclinado possível. Isso ocorre quando essa reta é tangente à curva:

Como podemos ver na figura, é mínimo quando é aproximadamente . Nesse ponto, é igual à derivada de :

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Nos exercícios de 39 a 42, uma partícula move-se ao longo de uma reta de acordo com a equação dada, onde s cm é a distância orientada da partícula até a origem, em t s. (a) Qual será a velocidade da p

Quando um pêndulo com 10 cm de comprimento balança, de modo que θ seja a medida em radianos do triângulo formado pelo pêndulo e uma reta vertical, então, se h θ cm for a altura da extremidade do pêndu

Ache uma equação da reta tangente à curva y = ( x 2 - 1 ) 2 em cada um dos seguintes pontos - 2 ,9 , - 1 ,0 ,0 ,1 ,1 ,0e( 2 ,9 ) . Faça um esboço do gráfico e desenhe segmentos das retas tangentes nos

A equação de demanda para um brinquedo é p 2 x = 5000 , onde x brinquedos são demandados por mês, quando p for o preço de cada unidade. Espera-se que em t meses, onde t ∈ [ 0,6 ] , o preço do brinqued

Em uma floresta, um predador alimenta-se de sua presa, e a população de predadores em qualquer época é uma função do número de presas naquele momento. Suponha que quando há x presas na floresta, a pop