Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 1.2 - Ex. 55

Ache as equações das três medianas do triângulo com vértices A(3, -2), B(3, 4) e C(-1, 1) e prove que elas se encontrar em um ponto.

Passo 1

Inicialmente vamos marcar os pontos no plano cartesiano e fazer o esboço do triângulo.

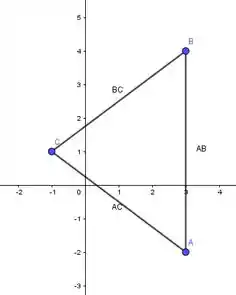
Como a mediana é o segmento que une um vértice ao ponto médio do lado oposto, precisamos achar o ponto médio de cada lado do triângulo.

→ Ponto médio de AB:

M A B = 3 + 3 2 , - 2 + 4 2 ⇒

M A B = 6 2 , 2 2 ⇒

M A B = 3 , 1

→ Ponto médio de AC:

M A C = 3 + ( - 1 ) 2 , - 2 + 1 2 ⇒

M A C = 2 2 , - 1 2 ⇒

M A C = 1 , - 1 2

→ Ponto médio de BC:

M B C = 3 + ( - 1 ) 2 , 4 + 1 2 ⇒

M B C = 2 2 , 5 2 ⇒

M B C = 1 , 5 2

Passo 2

Vamos determinar a inclinação da mediana que liga os pontos A e M B C .

m 1 = 5 2 - - 2 1 - 3 ⇒

m 1 = 5 2 + 2 1 - 3 ⇒

m 1 = 5 + 4 2 - 2 ⇒

m 1 = 9 2 - 2 ⇒

m 1 = 9 2 . - 1 2 ⇒

m 1 = - 9 4

Assim a equação da mediana que liga A e M B C é

y 1 - - 2 = - 9 4 x - 3 ⇒

y 1 + 2 = - 9 4 x - 3 ⇒

y 1 + 2 = - 9 x 4 + 27 4 ⇒

y 1 = - 9 x 4 + 27 4 - 2 ⇒

y 1 = - 9 x 4 + 27 - 8 4 ⇒

y 1 = - 9 x 4 + 19 4

Vamos determinar a inclinação da mediana que liga os pontos B e M A C .

m 2 = - 1 2 - 4 1 - 3 ⇒

m 2 = - 1 - 8 2 1 - 3 ⇒

m 2 = - 9 2 - 2 ⇒

m 2 = - 9 2 . - 1 2 ⇒

m 2 = 9 4

Assim a equação da mediana que liga B e M A C é

y 2 - 4 = 9 4 ( x - 3 ) ⇒

y 2 - 4 = 9 x 4 - 27 4 ⇒

y 2 = 9 x 4 - 27 4 + 4 ⇒

y 2 = 9 x 4 + - 27 + 16 4 ⇒

y 2 = 9 x 4 - 11 4

Vamos determinar a inclinação da mediana que liga os pontos C e M A B .

m 3 = 1 - 1 3 - - 1 ⇒

m 3 = 0 4 ⇒

m 3 = 0

Assim a equação da mediana que liga C e M A B é

y 3 - 1 = 0 x - - 1 ⇒

y 3 - 1 = 0 ⇒

y 3 = 1

Passo 3

Observe que se igualarmos y 1 = y 2 temos

y 1 = y 2 ⇒

- 9 x 4 + 19 4 = 9 x 4 - 11 4 ⇒

- 9 x 4 - 9 x 4 = - 11 4 - 19 4 ⇒

- 18 x 4 = - 30 4 ⇒

- 9 x 2 = - 15 2 ⇒

- 9 x = - 15 ⇒

x = - 15 - 9 ⇒

x = 15 9 ⇒

x = 5 3

Substituindo x = 5 3 em y 1 e em y 2 temos

y 1 =   - 9 4 . 5 3 + 19 4 ⇒

y 1 =   - 45 12 + 19 4 ⇒

y 1 =   - 15 4 + 19 4 ⇒

y 1 =   - 15 + 19 4 ⇒

y 1 =   4 4 ⇒

y 1 =   1

y 2 = 9 4 . 5 3 - 11 4 ⇒

y 2 = 45 12 - 11 4 ⇒

y 2 = 15 4 - 11 4 ⇒

y 2 = 15 - 11 4 ⇒

y 2 = 4 4 ⇒

y 2 = 1

Logo y 1 e y 2 se encontram no ponto 5 3 ,   1 .

Observe que y 1 e y 2 se encontram sobre a reta y 3 = 1 . Logo as três se encontram sobre o único ponto 5 3 ,   1 .

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Dê exemplo de uma função linear φ ( x , y ) = a x + b y , com a b ≠ 0 , tal que, para cc ' a distância entre as linhas de níveis cec ' de φ seja c ' - c
Qual é o ponto de ordenada 3 na reta paralela a 3 x - 2 y = 2 tirada pelo pontoA = ( 5 , - 1 ) ?
Dado o ponto ( x 0 , y 0 ) sobre a reta y = a x + b , determine α e β de modo que as equações x = α t + x 0 ,y = β t + y 0 sejam uma representação paramétrica da reta y = a x + b .
Seja a x + b y = c e a ' x + b ' y = c ' retas que têm um ponto P em comum. Prove que a reta a ' ' x + b ' ' y = c ' ' passa por este mesmo ponto P se, e somente se, existem n´umeros s, t tais que a '
Sejam A = (3, 5, 2) e B = (−1, −1, 4), C = (2, 1, 5) e D = (0, 3, 1). Mostre que as retas AB e CD têm um ponto em comum e determine este ponto P. Decida se P pertence a um dos segmentos de reta AB e C