Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 4.5 - Ex. 7
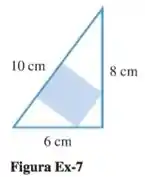
Resolva o Exercício 6, supondo o retângulo posicionado conforme a figura Ex-7.
Enunciado da questão 6:
Um retângulo deve ser inscrito em um triângulo retângulo com lados de comprimento 6, 8 e 10 cm. Encontre as dimensões do retângulo com a a maior área, supondo que ele está posicionado conforme a Figura Ex-6.
Passo 1
Esse é um típico exercício de otimização. O cálculo diferencial é uma ferramenta que nos ajuda muito na resolução desses casos, tão recorrentes no dia a dia.
Sempre esses exercícios precisam da sua boa interpretação de texto. No caso, queremos inserir um retângulo com a maior área possível, em uma posição específica, dentro do triângulo retângulo dado. Como fazer isso?
Passo 2
Comecemos por nomear nossas incógnitas. Vamos chamar de e os lados do retângulo da seguinte forma:
Como a gente quer a maior área possível pra esse retângulo, já escrevemos a expressão pra área dele, pois iremos usá-la! Temos pra área desse retângulo:
Aqui o problema é que está em função de duas incógnitas, mas, pra trabalhar essa função e achar seu valor máximo, precisamos escrever ela em função de uma só incógnita. Vamos fazer isso da seguinte forma:
Agora vamos trabalhar com as novas incógnitas e , de forma a estabelecer entre elas uma relação com as dimensões e que ainda não conhecemos.
Por semelhança de triângulos, trabalhando no maior triângulo formado entre o retângulo e o cateto de comprimento 6 cm, escrevemos:
Agora, no menor triângulo formado entre o retângulo e o cateto de comprimento 6 cm, temos:
Passo 3
Podemos agora aplicar Pitágoras no mesmo triângulo trabalhado no último passo do Passo 2. Pra ele, escrevemos o seguinte:
Substituímos em e as expressões que encontramos pra eles, em função de e , e teremos:
Trabalhamos um pouco essa expressão. Vamos ter:
Nisso, conseguimos uma expressão pra que o escreve em função de . Dessa forma, podemos pegar a expressão pra área do retângulo e escrever essa expressão que achamos no lugar de . Daí, determinamos a área em função apenas de !
Passo 4
Pra nova expressão da área, teremos:
Agora temos uma função que descreve a nossa área. Por nossos conhecimentos de funções, é descrita por uma parábola com concavidade voltada pra baixo. Logo, tem um ponto de máximo!
É esse ponto de máximo da área, desescrita em função de um de seus lados (lado ), que a gente precisa determinar. E como fazer isso?
Se você ainda não sabe, ou talvez não lembre, mas um dos teoremas do Cálculo (Teorema de Fermat) diz que, nos pontos de máximo e de mínimo de uma função (quando possui) a derivada se anula.
Logo, podemos pegar , derivar e igualar a zero! O valor de que acharmos atribuído a essa derivada nula vai ser o ponto em que a função assume o valor máximo. Em outras palavras, vamos achar o valor de , um dos lados do retângulo, que nos dá a maior área possível!
Passo 5
Derivando, temos:
Igualamos isso a zero:
Então, esse é o valor de , lado do retângulo, que vai possibilitar a maior área possível.
Temos , mas ainda precisamos de . Calculamos facilmente pela primeira equação!
Resposta
São as dimensões e .