Enunciado
Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 5.4 - Ex. 16
Ache a integral indefinida geral.
Passo 1
E aí, tudo certinho?
Nesse problema temos que calcular a integral dada por
Parece complicado?
Nesse caso de integração, não temos uma regra definida para se trabalhar com produtos, então só conseguimos integrar a função, manipulando-a de modo que possamos identificar integrais que conhecemos.
Desse modo, vamos aplicar a distributiva nesse produto:
Para facilitar ainda mais para nós, podemos usar a propriedade da integral da soma: a integral da soma é a soma das integrais:
Também precisaremos de uma tabela de primitivas, essa aqui:
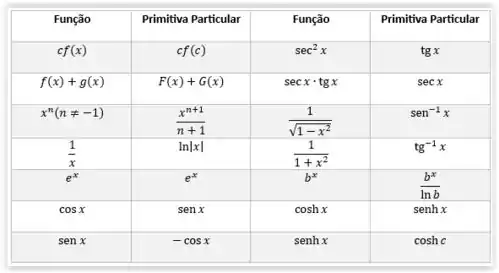
Agora sim estamos prontos!
Passo 2
Separando as integrais, temos:
Vamos resolver a primeira integral, olhando na tabela, temos a integral da função
Para a segunda, também olhando a tabela, temos:
E não esqueça das constantes ok?
Show?
Passo 3
Agora é só juntar tudo:
E aqui podemos juntar as constate em uma só!
Então voltando a nossa integral do início:
E aí! entendeu tudo? Responde Aí!
