Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 1.Revisão - Ex. 5
Ache e mostre na reta real o conjunto-solução da desigualdade.
Passo 1
Para isso, precisamos resolver a inequação para x. Quando não é uma reta, passamos todas as parcelas para o primeiro membro da desigualdade e comparamos com o para facilitar. E então analisamos as raízes das funções mais simples que aparecem para saber onde cada função assume valores positivos e negativos.
Passo 2
Assim,
Temos apenas uma função interessante para analisar: .
Passo 3
Para , temos
Passo 4
Agora, fazemos o esboço do seu gráfico para analisar o sinal da função: basta saber que é uma parábola com concavidade para cima (já que ).
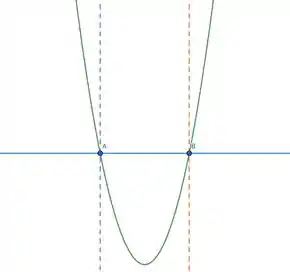
( e )
Passo 5
Podemos ver que e também que , que é o que nós queríamos.
Resposta
Exercícios de Livros Relacionados
Uma fornalha para a produção de cristais é usada em uma pesquisa para determinar a melhor maneira de manufaturar os cristais utilizados em componentes eletrônicos para os veículos espaciais. Para a pr
Quão próximo de - 3 devemos tomar x para que 1 x + 3 410000
Resolva a inequação. 3 x + 3x + 6
Resolva a inequação. 2 x + 1 ≥ 3 x
Resolva a inequação. x + 3 ≤ 6 x - 2