Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 4.1 - Ex. 47
Ache o valor máximo absoluto e o valor mínimo absoluto da função dada no intervalo indicado pelo método usado nos Exemplos 3 e 4 desta secção. Faça um esboço do gráfico da função no intervalo.
Passo 1
Vamos fazer o exercício do jeito que ele, usando o Teorema do Valor Extremo. Esse teorema diz que se uma função é continua em um intervalo fechado, ela terá um máximo absoluto e um mínimo absoluto nesse intervalo fechado. Vamos seguir o mesmo passo a passo que o livro usa nos exemplos 3 e 4:
- Ache os valores dos números críticos de em
- Ache os valores de e
- O maior dos dois valores será o máximo absoluto e o menor valor será o mínimo absoluto
Passo 2
Derivando a , ficamos com:
E como a derivada de :
Passo 3
Agora precisamos dos valores onde
Ou seja:
Então:
Onde
Passo 4
Então vamos precisar de um que esteja presente no intervalo e que satisfaça a equação que encontramos acima. Podemos fazer e na equação acima e ficaremos com:
Esses são os pontos críticos da nossa função!
Passo 5
Agora vamos calcular o valor de nos pontos que achamos:
E
Que já era de se esperar, porque temos uma função seno de amplitude .
Passo 6
Como diz o 3º passo do nosso passo a passo, o menor dos dois valores será o mínimo absoluto e maior valor sera o máximo absoluto do intervalo, daí temos:
Mín. absoluto:
Máx. absoluto:
Passo 7
O gráfico dessa função no intervalo é um seno de amplitude e fase . Sem stress!
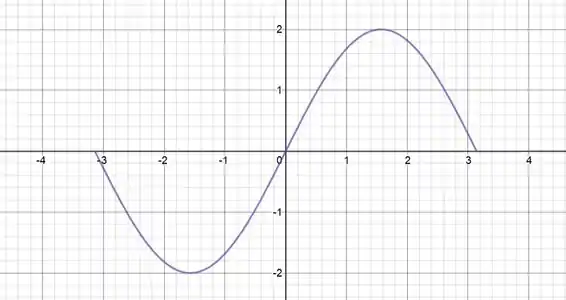
Use os valores de máximo e mínimo que encontramos para facilitar a vida quando for esboçar o gráfico ;)
Resposta
Mín. absoluto:
Máx. absoluto:
