Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Diva Flemming - Cálculo A- Ed: 6º - Capítulo 5.10 - Ex. 9k

Encontrar os pontos de máximo e mínimo relativos da seguinte função, se existirem. Fazer um esboço do gráfico e comparar os resultados.

f x = x + 2 2 x - 1 3

Passo 1

Para calcular os valores máximos e mínimos de uma função de forma simplificada primeiro precisamos calcular sua primeira derivada, iguala-la a zero e isolar a variável x .

Assim, derivando f ( x ) pela Regra do Produto, temos que:

f ' x = 2 x + 2 x - 1 3 + 3 x - 1 2 x + 2 2

Lembre-se que a Regra do Produto é dada por: derivada do primeiro (primeira parcela) vezes o segundo (segunda parcela) mais a derivada do segundo (segunda parcela) vezes o primeiro (primeira parcela).

Passo 2

Igualando o resultado de f ' ( x ) a zero e simplificando, temos:

f ' x = 0 ⇒ 2 x + 2 x - 1 3 + 3 x - 1 2 x + 2 2 = 0 ⇒

x - 1 2 3 x + 2 2 + 2 x - 1 x + 2 = 0 ⇒

x - 1 2 [ 3 x 2 + 12 x + 12 + 2 x 2 + 2 x - 4 ] = 0 ⇒

x - 1 2 5 x 2 + 14 x + 8 = 0 ⇒ x - 1 2 x + 4 5 x + 2 = 0

Assim, x = 1 ,   x = - 4 5     e     x = - 2 , são pontos críticos.

Passo 3

Pelo teste da primeira derivada, temos que:

f ' x = x - 1 2 5 x 2 + 14 x + 8 > 0

x - 1 2 ≥ 0

5 x 2 + 14 x + 8 > 0 ⇒ x < - 2   o u   x > - 4 5

Portanto, x = - 2 é ponto de máximo e x = - 4 5 é ponto de mínimo.

x = 1 não é ponto de máximo nem de mínimo.

Passo 4

Analisando o gráfico da função f ( x ) , temos que:

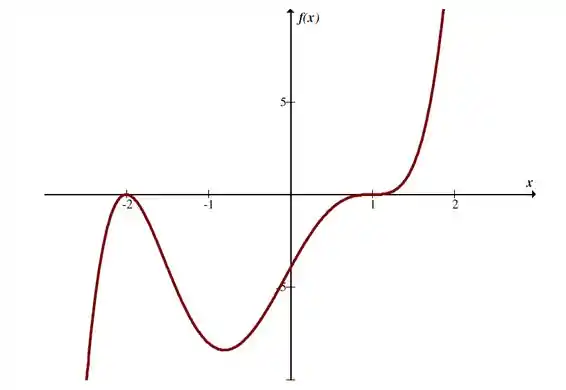
Logo, visualizamos que - 2 é um ponto de máximo e - 4 5 é um ponto de mínimo.

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Suponha que f admite derivada de 3º ordem contínua no intervalo aberto I e seja p ∈I . Prove que se f ' p = f ' ' p = 0 e f ' ' ' p ≠ 0 então p é um ponto de inflexão horizontal.
Generalise os resultados obtidos nos exércícios 2 e 3
Suponha g derivável em [a,b] e seja m tal que g ’ ( a )mg ’ ( b ) . Prove que existe x em ]a,b[ tal g ’ ( c ) = m
Seja y = f ( x ) uma função derivável até a 2ª. Ordem no intervalo aberto I, tal que para todo x ∈ I f ' ' x + x f ' x - f x 2 = 0 f x ≠ 0 Verifique que f’’ é continua em I Prove que a função f não di
Encontre os valores máximo e mínimo locais de f usando Testes da Primeira e Segunda Derivadas. Qual método você prefere? f x = x -x 4