Ache o valor máximo absoluto e o valor mínimo absoluto da função dada no intervalo indicado pelo método usado nos Exemplos 3 e 4 desta secção. Faça um esboço do gráfico da função no intervalo.
Passo 1
Vamos seguir um passo a passo tranquilo pra resolver esses problemas, da mesma forma que o livro faz nos exemplos 3 e 4 desta seção.
- Determinar a derivada da função.
- Fazer e depois encontrar os valores de para os quais não existe.
- Achar os valores de que satisfazem as proposições acima e estão dentro do intervalo especificado.
- Dos valores encontrados, o menor vai ser o mínimo absoluto e o maior será o máximo absoluto do intervalo.
- Esboçar o gráfico utilizando os valores de máximo e mínimo que temos.
Vamo devagarinho que dá bom!
Passo 2
Vamos começar achando a derivada desse quociente de polinômios do 1º grau:
Pela regra do quociente:
Vamos analisar a derivada que encontramos para conseguir mais informação sobre a nossa função. Como o termo de está ao quadrado, ele sempre será positivo, mas temos um sinal negativo do lado de fora, ou seja, a derivada é sempre negativa! Isso quer dizer que a função é sempre decrescente. Além disso, a derivada nunca se iguala a ! Então não podemos definir os extremos a partir daquele teorema.
Passo 3
Isso não irá nos impedir de encontrar o máximo e o mínimo absoluto dessa função no intervalo dado! Pensa comigo: temos uma função que está sempre diminuindo, como se fosse uma exponencial decrescente, se escolhemos um intervalo fechado dessa função, onde estarão os máximos e os mínimos absolutos? Nos extremos! Pois como a função só faz diminuir, podemos concluir que o máximo absoluto está em e o mínimo absoluto está em !.
Então nosso máximo absoluto será em e o mínimo absoluto será em !
Passo 4
Calculando o valor da função nesses dois pontos:
E
Passo 5
Da equação que temos, podemos ver que a função tende a em . Então vamos ter um gráfico que vai de até cada vez mais íngreme (já que a derivada é inversamente proporcional a ). O nosso gráfico vai ficar:
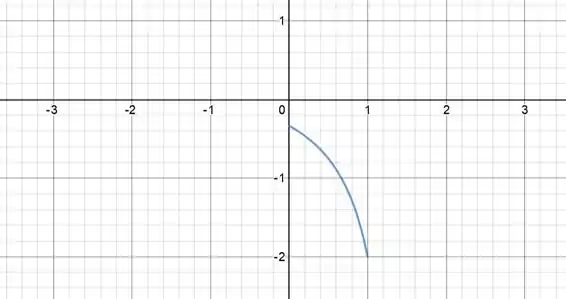
Resposta
Mín. absoluto:
Máx. absoluto: