Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 4.1 - Ex. 56
Ache o valor máximo absoluto e o valor mínimo absoluto da função dada no intervalo indicado pelo método usado nos Exemplos 3 e 4 desta secção. Faça um esboço do gráfico da função no intervalo.
Passo 1
Como a função é condicional, ela provavelmente não segue a mesma regra das outras funções que só tem uma equação. Como ela muda de comportamento a partir de outra equação, vamos fazer o gráfico da função e ver como ele pode nos ajudar a determinar os máximos e mínimos absolutos da função.
Lembre-se da equação de uma parábola genérica com vértice em :
O sinal positivo ou negativo fora do parêntese vai determinar a concavidade da parábola.
: Concavidade para cima
: Concavidade para baixo
Vamos usar essas coisas para plotar o gráfico da nossa função com amor e carinho
Passo 2
A 1ª equação da nossa função nos dá:
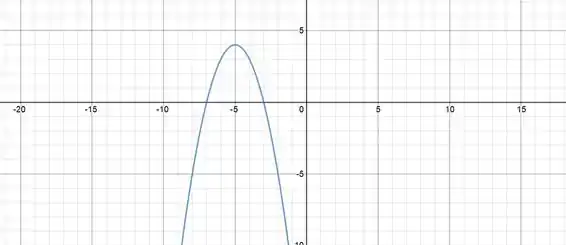
Temos uma parábola! Ela tem concavidade para baixo por causa do sinal negativo e seu vértice é em :
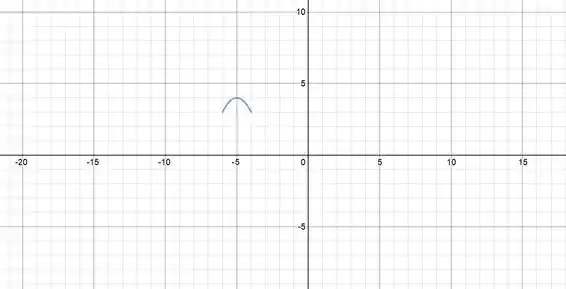
Mas só queremos ela no intervalo . Ficamos então com esse pedaço da parábola:
Passo 3
No segundo caso da função temos outra parábola:
Ela também tem concavidade para baixo e seu vértice está em . No gráfico isso fica:
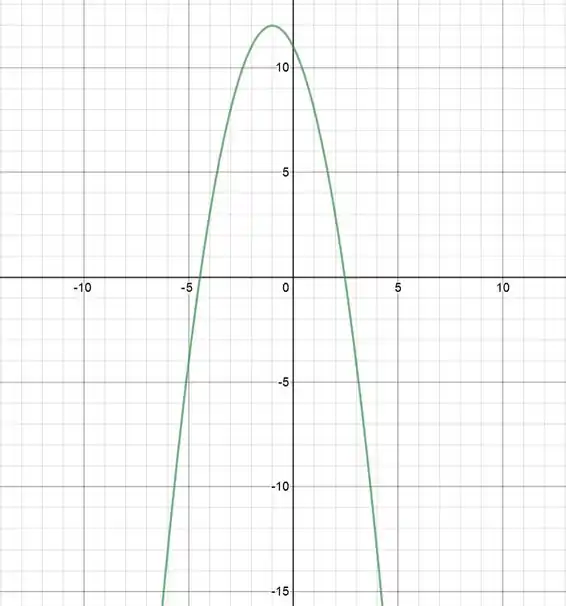
Mas isso só vale para . Vamos restringir o nosso domínio então:
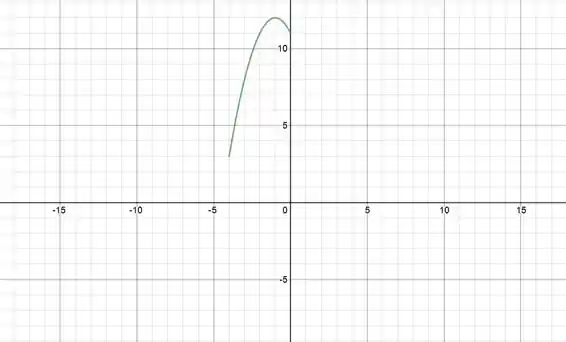
Passo 4
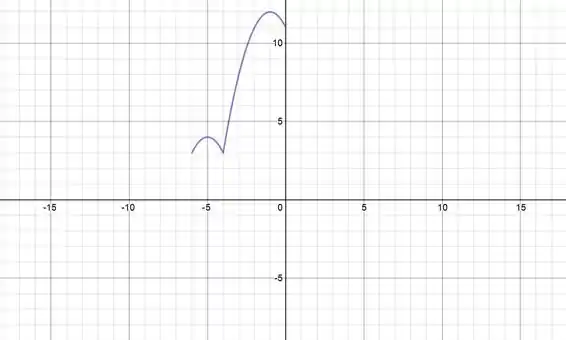
Agora juntando os dois gráficos que encontramos teremos o gráfico da função!
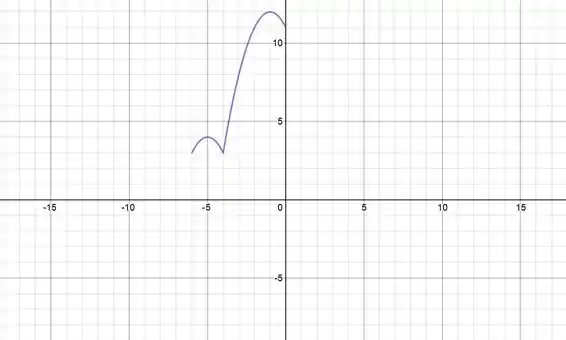
Agora vamos analisar os máximos e mínimos da função.
Passo 5
Pelo gráfico vemos que o ponto de máximo é o ponto do vértice da 2ª parábola que já encontramos antes:
O mínimo da função é meio ambíguo, não podemos afirmar se o mínimo está no extremo esquerdo do intervalo ou se ele está na junção das duas parábolas. Vamos verificar fazendo o valor da função em cada um dos respectivos pontos: e /
Os dois pontos têm o mesmo valor! Então os dois são os mínimos globais da função.
Resposta
Mín. absoluto:
Máx. absoluto:
