Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 3.2 - Ex. 31
31. Ache os valores de a e b tais que seja derivável em 2 se
Passo 1
Uma função f definida num intervalo aberto que contém x1 será derivável em x1 se e somente se 
ambas existirem e forem iguais. E se ela for derivável em x1, necessariamente ela é contínua em x1.
Na questão ele nos pede para encontrarmos duas constantes, a e b, para que f(x) seja derivável em x1 = 1. Porém, para provar isso devemos determinar a derivada à esquerda e à direita de f (x) em x1 = 1, para vê se a condição para que ela seja derivável é aceita.
A derivada à esquerda de f em x1, denotada por f’ - (x1), será definda por
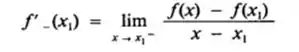
A derivada à direita de f em x1, denotada por f’ + (x1), será definda por
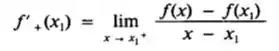
Passo 2
A derivada à esquerda de f(X) em x1 = 2 será:
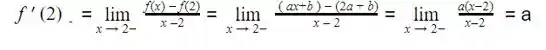
Passo 3
A derivada à direita de f(X) em x1 = 2 será :
Logo, para que f seja derivável a sua derivada à esquerda deve ser igual a derivada à direita. Com isso temos que a = 8. Para acharmos o valor de b , temos que encontrar uma relação entre a e b utilizando-se do conceito de continuidade, pois para que ela seja derivável em x = 2 ela deve ser contínua em x = 2. Dizer que f é contínua em x = 2 é a mesma coisa que afirmar que o limite nesse ponto é igual ao valor da função nesse ponto. Assim, temos:
Passo 4
Para acharmos o valor de b , temos que encontrar uma relação entre a e b utilizando-se do conceito de continuidade, pois para que ela seja derivável em x = 2 ela deve ser contínua em x = 2. Dizer que f é contínua em x = 2 é a mesma coisa que afirmar que o limite nesse ponto é igual ao valor da função nesse ponto. Assim, temos:
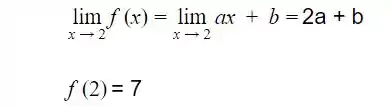
Entao, para que f seja contínua obtemos a seguinte relação entre a e b
2a + b =7
Portanto, temos que b = -9.
Resposta
a = 8 e b = -9.