Um funil com um dado volume deve ter a forma de um cone circular reto. Ache a razão entre a altura e o raio da base se a quantidade de material usado em suan fabricação for mínima.
Passo 1
Visualizar o problema
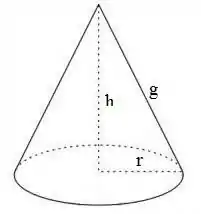
Passo 2
Nosso problema é de otimização. Dado um volume FIXO, queremos a Menor Area.
Sabendo que :
Volume Cone = 1/3 h . Area da Base = (I)
Area Lateral Cone = (II)
Passo 3
Podemos usar pitagoras para encontrar g .
Logo
g² = h² + r²
g = (III)
Assim, usando (II) em (II) temos :
ACone=
Nossa intenção é Derivar Acone e igualar a zero para encontrar a otimização. Porem A é uma função de h e r , ou seja , A(h,r). Assim temos que achar alguma outra relação que faça uma variável seja função da outra
Visto que Temos um volume fixo, então podemos pegar a equação (I) e igualar a uma constante arbitraria. Logo :
Assim temos que h = .
Pronto , fizemos h ser função de r.
Passo 4
Nossa função de Area lateral fica agora
ACone= =
Agora podemos otimizar nossa função.
Um truque que pode nos ajudar
Tem a mesma solução . Logo, por ser mais fácil , vou derivar a equação (V)
Passo 5
Queremos a razão h/r
Sabendo que h = , podemos dizer que r² =
Logo h =
Assim h/r = =
Resposta
h/r =