Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 4.8 - Ex. 48
A seção transversal de uma tina tem a forma de um triangulo isósceles invertido. Se o comprimento dos lados iguais for de 15 cm , ache a medida do ângulo do vértice que dará capacidade máxima à tina.
Passo 1
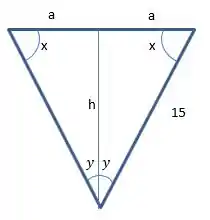
Figura 1
Passo 2
Temos que algumas relação de trigonometria :
2y + 2x = 180 (II)
a² + h² = 15² (III)
Queremos descobrir o valor de 2y que nos dê a maior área
Podemos fazer que cos y = h/15 (IV)
Usando (IV) em (III) :
a² + (15 cos y)² = 15²
a² = 15² - 15²cos²y
a² = 15²(1-cos²y)
Usando a relação (I)
a² = 15² sen²y
a= 15seny (V)
A área de triangulo é b.h/2
NO nosso Caso, usando as relações (IV) e (V) , temos que A =
A(y) =
Sabendo que
Temos que A(y) =
Otimizando A(y). Ou seja ,
Cos2y=0
2y =
Resposta
2y =
Ou seja o ângulo do vértice da tina de maior área é
Exercícios de Livros Relacionados
Ache, com até quatro casas decimais, o valor de x no intervalor ( π 2 , 3 π 2 ) para o qual tg x = x, aplicando o método de Newton.
Traçe o esbolço do gráfico de uma função f no intervalo I em cada caso: (a) I é um intervalo aberto (0,2) e f é contínua em I. Em 1, f tem um valor máximo relativo, mas f ' ( 1 ) não existe. (b) I é o
Sejam f e g duas funções diferenciáveis em todo número no intervalo fechado [a,b]. Suponha, então, que f a = g ( a ) e f b = g ( b ) . Prove que existe um número c no intervalo aberto (a,b); tal que f
Suponha que c x = x 3 - 20 x 2 + 20000 x se já o custo para manufaturar x itens. Determine o nível de produção que minimizará o custo médio para produzir x itens.
Demonstre que se a , b , c e d são interios positivos, então: a 2 + 1 b 2 + 1 c 2 + 1 d 2 + 1 a b c d ≥ 16