Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 4.7 - Ex. 51
Uma refinaria de petróleo está localizada na margem norte de um rio reto que tem de largura. Um oleoduto deve ser construído da refinaria até um tanque de armazenamento localizado na margem sul do rio, a leste da refinaria. O custo de construção é sobre a terra, até um ponto na margem norte e sob o rio até o tanque. Onde deveria estar localizado para minimizar o custo do oleoduto?
Passo 1
Fala, galera! Beleza? Vamos resolver essa questão!
O enunciado pediu pra gente encontrar a localização do ponto que minimizaria o custo da construção do oleoduto. Nós sabemos que a refinaria está localiza na margem norte de um rio reto que tem de largura e que o oleoduto deve ser construído da refinaria até um tanque de armazenamento localizado na margem sul do rio, a leste da refinaria.
Além disso, ele nos fala que o custo de construção é sobre a terra, até um ponto na margem norte e sob o rio até o tanque.
Com as informações esboçamos a seguinte imagem:
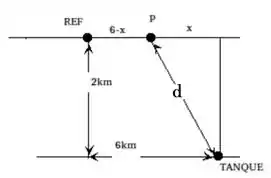
O que nós vamos fazer é escrever uma expressão para o custo dessa construção e minimizar a função encontrada através da derivação.
Vamos lá!
Passo 2
O que queremos é minimizar a função custo, que pode ser escrita da seguinte forma:
A função está dependendo de duas variáveis, então vamos isolar em função de , usando a fórmula da distância entre dois pontos:
Assim, temos:
Substituindo em , encontramos:
Passo 3
Agora para minimizar , vamos começar derivando nossa função:
E igualando isso a zero:
Elevando os dois lados ao quadrado:
E isolando :
se encontra a uma distância de da refinaria, então, deve estar em: a leste da refinaria.
Valeu, galera! Até a próxima! 😉