Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 9.4 - Ex. 36

Ache o volume do sólido gerado pela rotação da região abaixo (região do exercício 34) em torno do eixo y .

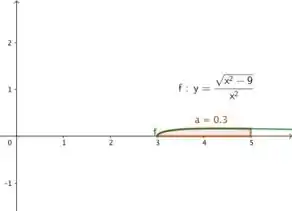
Passo 1

Pessoal, como vai ser a rotação em torno do eixo y e temos uma função na variável x , está perfeito para usarmos o método dos invólucros cilíndricos, ok?

Agora para resolver, a primeira coisa a se fazer é lembrar a fórmula que calcula o volume sólido obtido pela rotação da curva f ( x ) em um intervalo [ a , b ] .

V = 2 π ∫ a b r x h ( x ) d x

Sempre quando a rotação é em torno do eixo y , usando o método dos invólucros, o r x = x e nossa h x = f x = x 2 - 9 x 2 , pois será área entre ela e o eixo x . O intervalo de integração será de x = 3 a reta x = 5 . Sendo assim, o volume será dado por:

V = 2 π ∫ 3 5 x x 2 - 9 x 2 d x = 2 π ∫ 3 5 x 2 - 9 x d x

Passo 2

Podemos resolver essa integral de duas formas: calcular a indefinida e no final resolver a definida ou ir resolvendo direto trocando os limites de integração.

Nesta questão, nós vamos resolver a definida, no caminho, trocando os limites de integração, ok? Agora, para resolver, vamos precisar saber qual substituição trigonométrica usar.

Como nós temos a expressão x 2 - 9 = x 2 - 3 2 , isso indica a substituição com a secante, como vocês podem ver a seguir no quadro de substituições com os respectivos triângulos e intervalos.

Olhando o quadrinho, percebemos que a substituição deve ser x = 3 sec ⁡ θ .

Passo 3

Façamos então a substituição:

x = 3 sec ⁡ θ d x = 3 sec ⁡ θ tan ⁡ θ d θ

Dessa forma, x 2 = 9 sec 2 ⁡ θ     →     x 2 - 9 = 9 sec 2 ⁡ θ - 9 = 9 sec 2 ⁡ θ - 1 ⏞ tan 2 ⁡ θ = 3 2 tan 2 ⁡ θ .

Passo 4

Agora vamos trocar a variável da integral, mas antes vamos obter os limites de integração na variável θ . Seja então:

x = 3 → 3 = 3 sec ⁡ θ →           1 = sec ⁡ θ     →         θ = 0 x = 5 → 5 = 3 sec ⁡ θ →         θ = sec - 1 ⁡ 5 3

Substituindo tudo na integral, ficamos com:

V = 2 π ∫ 3 5 x 2 - 9 x d x = 2 π ∫ 0 sec - 1 ⁡ 5 3 3 2 tan 2 ⁡ θ 3 sec ⁡ θ 3 sec ⁡ θ tan ⁡ θ d θ = 6 π ∫ 0 sec - 1 ⁡ 5 3 tan 2 ⁡ θ d θ

V = 6 π ∫ 0 sec - 1 ⁡ 5 3 ( sec 2 ⁡ θ - 1 ) d θ

Prontinho!

Passo 5

Agora vamos resolver a definida.

Sabemos da integral definida que:

∫ a b f x d x = F b - F a

Em que F é uma primitiva de f .

Dessa forma, utilizando a integral ∫ sec 2 ⁡ θ d θ = tan ⁡ θ + C , ficamos com:

V = 6 π ∫ 0 sec - 1 ⁡ 5 3 ( sec 2 ⁡ θ - 1 ) d θ = 6 π tan ⁡ θ - θ 0 sec - 1 ⁡ 5 3

V = 6 π tan ⁡ sec - 1 ⁡ 5 3 - sec - 1 ⁡ 5 3 - tan ⁡ 0 - 0

Passo 6

Para achar tan ⁡ sec - 1 ⁡ 5 3 vamos usar a relação:

tan 2 ⁡ sec - 1 ⁡ 5 3 ⏟ x + 1 = sec 2 ⁡ sec - 1 ⁡ 5 3 ⏟ x = 5 3 2

tan 2 ⁡ sec - 1 ⁡ 5 3 = 25 9 - 1 = 16 9

tan ⁡ sec - 1 ⁡ 5 3 = 4 3     pois       0 ≤ sec - 1 ⁡ 5 3 < π 2

Passo 7

Agora podemos simplificar o resultado achado.

V = 6 π tan ⁡ sec - 1 ⁡ 5 3 - sec - 1 ⁡ 5 3 - tan ⁡ 0 - 0 = 6 π 4 3 - sec - 1 ⁡ 5 3 = 8 π - 6 π sec - 1 ⁡ 5 3   u . v

Logo, o volume é V = 8 π - 6 π sec - 1 ⁡ 5 3   u . v .

Resposta

V = 8 π - 6 π sec - 1 ⁡ 5 3   u . v

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Encontre o volume do sólido obtido pela rotação da região delimitada pelas curvas dadas em torno das retas especificadas. Esboce a região. y = 1 - x 2 ,y = 0 ; e mt o r n od oe i x ox
Encontre uma integral para o volume do sólido obtido pela rotação da região delimitada pelas curvas dadas sobre a reta especificada. Em seguida, use a calculadora para determinar a integral com precis
Encontre uma integral para o volume do sólido obtido pela rotação da região delimitada pelas curvas dadas sobre a reta especificada. Em seguida, use a calculadora para determinar a integral com precis
Encontre o volume do sólido obtido pela rotação da região delimitada pelas curvas dadas em torno das retas especificadas. Esboce a região. y = 1 4 x 2 ,y = 5 - x 2 ; e mt o r n od oe i x ox
Encontre o volume do sólido obtido pela rotação da região delimitada pelas curvas dadas em torno das retas especificadas. Esboce a região. y = 1 4 x 2 ,x = 2 ,y = 0 ; e mt o r n od oe i x oy