Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 6.2 - Ex. 10
Encontre o volume do sólido obtido pela rotação da região delimitada pelas curvas dadas em torno das retas especificadas. Esboce a região.
Passo 1
Opa, bora resolver esse problema! O enunciado nos dá as seguintes curvas
E pede pra a gente calcular o volume do sólido obtido pela rotação em torno do eixo da região delimitada pelas curvas acima! Depois disso temos que esboçar a região!
Antes de qualquer coisa a gente precisa conseguir visualizar o problema. Então vamos esboçar o gráfico das curvas dadas! Temos uma parábola:
E duas retas:
Ficamos com:
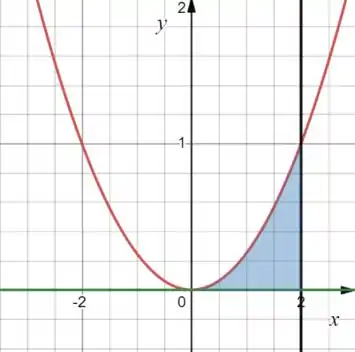
A área que a gente vai rotacionar em torno do eixo é essazinha de azul!
Passo 2
Como estamos falando de uma área de rotação, ela vai ser circular . E como ela vai estar entre 2 funções, então vamos subtrair uma da outra
Lembrando que cada função representa um raio, logo:
Assim,
Podemos calcular o volume. Os limites de integração vão ser os pontos de intersecção entre as curvas! Temos:
O nosso limite de integração superior vai ser e o inferior .
Passo 3
Resolvendo a integral, temos:
Passo 4
Pra acabar vamos desenhar a região:
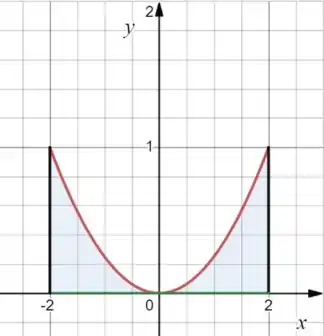
Prontinho!